
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若![]() ,则△A6B6A7的边长为( )
,则△A6B6A7的边长为( )
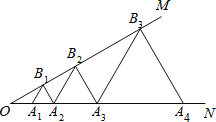
A.6B.12C.16D.32
【答案】C
【解析】
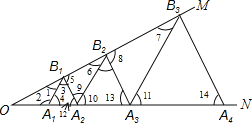
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2,A4B4=8B1A2,A5B5=16B1A2…进而得出答案.
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=![]() ,
,
∴A2B1=![]() ,
,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,
…
∴△AnBnAn+1的边长为![]() ×2n﹣1,
×2n﹣1,
∴△A6B6A7的边长为![]() ×26﹣1=
×26﹣1=![]() ×25=16.
×25=16.
故选:C.


科目:初中数学 来源: 题型:
【题目】已知:如图,AB为半圆O的直径,C是半圆O上一点,过点C作AB的平行线交⊙O于点E,连接AC、BC、AE,EB. 过点C作CG⊥AB于点G,交EB于点H.
(1)求证:∠BCG=∠EBG;
(2)若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
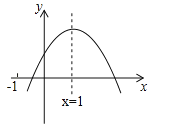
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①abc>0,
②a﹣b+c<0,
③2a=b,
④4a+2b+c>0,
⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .
.
其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
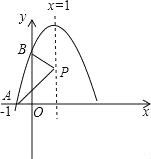
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
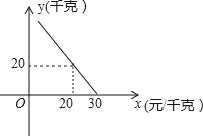
【题目】五家尧草莓是我旗的特色农产品,深受人们的喜欢.某超市对进货价为10元/千克的某种草莓的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)为了让顾客得到实惠,商场将销售价定为多少时,该品种草莓每天销售利润为150元?
(3)应怎样确定销售价,使该品种草莓的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连结AP和AQ,且BP=PQ=QC.求∠C的度数.
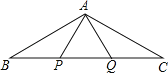
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA= ,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ= (等量代换)
∴△APQ是 三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠ .
又∵∠AQP是△AQC的外角,
∴∠AQP=∠ +∠ =60°.(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
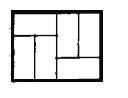
【题目】如图,由6个长为2,宽为1的小矩形组成的大矩形网格,小矩形的顶点称为这个矩形网格的格点,由格点构成的几何图形称为格点图形(如:连接2个格点,得到一条格点线段;连接3个格点,得到一个格点三角形;…),请按要求作图(标出所画图形的顶点字母).
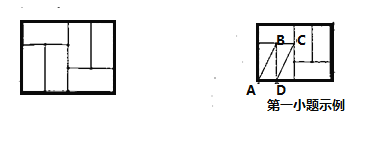
(1)画出4种不同于示例的平行格点线段;

(2)画出4种不同的成轴对称的格点三角形,并标出其对称轴所在线段;

(3)画出1个格点正方形,并简要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com