
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
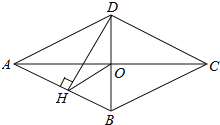
A.20°B.25°C.30°D.40°
【答案】A
【解析】
先根据菱形的性质得OD=OB,AB∥CD,BD⊥AC,则利用DH⊥AB得到DH⊥CD,∠DHB=90°,所以OH为Rt△DHB的斜边DB上的中线,得到OH=OD=OB,利用等腰三角形的性质得∠1=∠DHO,然后利用等角的余角相等即可求出∠DHO的度数.
解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠1=∠DHO,
∵DH⊥CD,
∴∠1+∠2=90°,
∵BD⊥AC,
∴∠2+∠DCO=90°,
∴∠1=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故选A.



 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,D,E分别是△ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称弧DE为△ABC的中内弧.例如,图1中弧DE是△ABC其中的某一条中内弧.
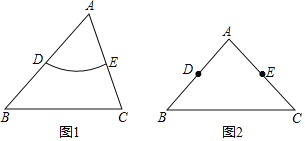
(1)如图2,在边长为4![]() 的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
(2)在平面直角坐标系中,已知点A(2![]() ,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
①若t=2![]() ,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
②请写出一个t的值,使得△ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
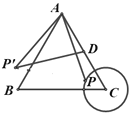
【题目】如图,等边三角形ABC中,AB=4cm,以C为圆心,1cm长为半径画⊙C,点P在⊙C上运动,连接AP,并将AP绕点A顺时针旋转60°至AP′,点D是边AC的中点,连接DP′.在点P移动的过程中,线段DP′长度的最小值为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=α,将△ABC绕点C顺时针方向旋转到△A′B′C的位置,使AA′∥BC,设旋转角为β,则α,β满足关系( )
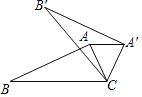
A.α+β=90°B.α+2β=180°C.2α+β=180°D.α+β=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块三角形材料,∠A=30°,∠C=90°,AB=6.用这块材料剪出一个矩形DECF,点D,E,F分别在AB,BC,AC上,要使剪出的矩形DECF面积最大,点D应该选在何处?
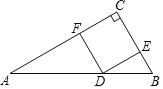
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.若∠AOD=120°,AC=4,则CD的大小为( )
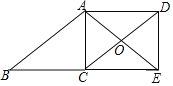
A.8B.4![]() C.8
C.8![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值:
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:思考的同学小斌在解决连比等式问题:“已知正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值”时,采用了引入参数法
的值”时,采用了引入参数法![]() ,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出
,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出![]() ,
,![]() ,
,![]() 之间的关系,从而解决问题.过程如下:
之间的关系,从而解决问题.过程如下:
解;设![]() ,则有:
,则有:
![]() ,
,![]() ,
,![]() ,
,
将以上三个等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都为正数,
都为正数,
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔细阅读上述材料,解决下面的问题:
(1)若正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求证:
互不相等,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com