
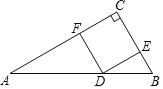
【题目】如图,是一块三角形材料,∠A=30°,∠C=90°,AB=6.用这块材料剪出一个矩形DECF,点D,E,F分别在AB,BC,AC上,要使剪出的矩形DECF面积最大,点D应该选在何处?
科目:初中数学 来源: 题型:
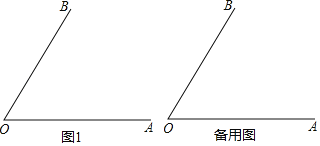
【题目】已知∠AOB=60°,P为它的内部一点,M为射线OA上一点,连接PM,以P为中心,将线段PM顺时针旋转120°,得到线段PN,并且点N恰好落在射线OB上.
(1)依题意补全图1;
(2)证明:点P一定落在∠AOB的平分线上;
(3)连接OP,如果OP=2![]() ,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
查看答案和解析>>
科目:初中数学 来源: 题型:
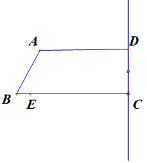
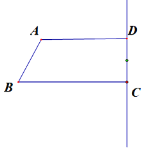
【题目】如图:四边形ABCD中,AD∥BC,∠ADC=90°,AD=4,CD=2,BC=5,点E在BC边上自B向C运动(不与点C重合),连接AE,过点E作AE的垂线交直线CD于F点.设BE的长为![]() ,CF的长为
,CF的长为![]() .
.
(1) 求![]() 的值
的值
(2) 求![]() 的长,(用含
的长,(用含![]() 的代数式表示)
的代数式表示)
(3) 连接AF,在点E运动的过程中,△![]() 的外心
的外心![]() 点的位置也随之变化,探索:
点的位置也随之变化,探索:![]() 满足什么条件,外心
满足什么条件,外心![]() 落在四边形ABCD的边上或形外.
落在四边形ABCD的边上或形外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
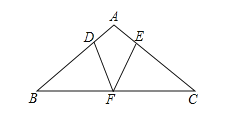
(1)求证:△BDF≌△CEF.
(2)当∠A= 100°,BD=BF时,求∠DFE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
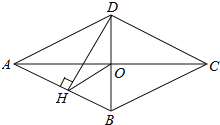
A.20°B.25°C.30°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

(1)求证:四边形AFBD是平行四边形;
(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
①当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米. 点
厘米. 点![]() 沿
沿![]() 边从
边从![]() 开始向点
开始向点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以1厘米/秒速度移动.如果
以1厘米/秒速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间
(秒)表示移动的时间![]() ,那么:
,那么:
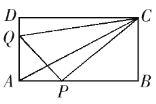
(1)当![]() 为何值时,
为何值时,![]() 为等腰直角三角形?
为等腰直角三角形?
(2)求四边形![]() 的面积;提出一个与计算结果有关的结论;
的面积;提出一个与计算结果有关的结论;
(3)当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com