
【题目】我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.
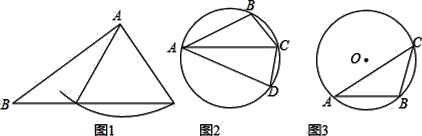
(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;
(2)如图3,△ABC内接于⊙O,⊙O的半径为![]() ,AB=6,∠BAC=30°,求AC的长;
,AB=6,∠BAC=30°,求AC的长;
(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求![]() 的值.
的值.
【答案】(1)详见解析;(2)3![]() +3;(3)
+3;(3)![]() =
=![]() 或
或![]() .
.
【解析】
(1)由点C是弧BD的中点,根据弧与弦的关系,易得BC=CD,∠BAC=∠DAC,又由公共边AC,可证得:△ABC和△ACD是同族三角形;
(2)首先连接0A,OB,作点B作BE⊥AC于点E,易得△AOB是等腰直角三角形,继而求得答案;
(3)分别从当CD=CB时与当CD=AB时进行分析求解即可求得答案.
(1)证明:∵点C是弧BD的中点,即![]() ,
,
∴BC=CD,∠BAC=∠DAC,
∵AC=AC,
∴△ABC和△ACD是同族三角形.
(2)解:如图1,连接OA,OB,作点B作BE⊥AC于点E,
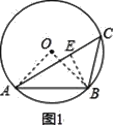
∵OA=OB=3![]() ,AB=6,
,AB=6,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,且∠AOB=90°,
∴∠C=∠AOB=45°,
∵∠BAC=30°,
∴BE=AB=3,
∴AE=![]() =3
=3![]() ,
,
∵CE=BE=3,
∴AC=AE+CE=3![]() +3.
+3.
(3)解:∵∠B=180°﹣∠BAC﹣∠ACB=180°﹣30°﹣45°=105°,
∴∠ADC=180°﹣∠B=75°,
如图2,当CD=CB时,∠DAC=∠BAC=30°,
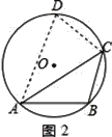
∴∠ACD=75°,
∴AD=AC=3![]() +3,CD=BC=
+3,CD=BC=![]() BE=3
BE=3![]() ,
,
∴![]() =
=![]() ;
;
如图3,当CD=AB时,过点D作DF⊥AC,交AC于点F,
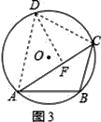
则∠DAC=∠ACB=45°,
∴∠ACD=180°﹣∠DAC﹣∠ADC=60°,
∴DF=CDsin60°=6×![]() =3
=3![]() ,
,
∴AD=![]() DF=
DF=![]() ,
,
∴![]() =
=![]() .
.
综上所述:![]() =
=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D,E分别是△ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称弧DE为△ABC的中内弧.例如,图1中弧DE是△ABC其中的某一条中内弧.
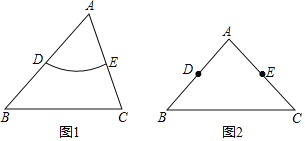
(1)如图2,在边长为4![]() 的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
(2)在平面直角坐标系中,已知点A(2![]() ,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
①若t=2![]() ,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
②请写出一个t的值,使得△ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.

请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
⑴.求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑵.求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑶.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
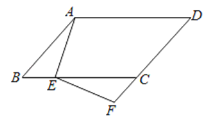
(1) 求证:△ABE∽△ECF;
(2) 若AB=5,AD=8,BE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com