
【题目】如图,在![]() ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
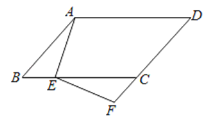
(1) 求证:△ABE∽△ECF;
(2) 若AB=5,AD=8,BE=2,求FC的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由平行四边形的性质可知AB∥CD,AD∥BC.所以∠B=∠ECF,∠DAE=∠AEB,又因为又∠DAE=∠F,进而可证明:△ABE∽△ECF;
(2)由(1)可知:△ABE∽△ECF,所以![]() ,由平行四边形的性质可知BC=AD=8,所以EC=BCBE=82=6,代入计算即可.
,由平行四边形的性质可知BC=AD=8,所以EC=BCBE=82=6,代入计算即可.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B=∠ECF,∠DAE=∠AEB.
又∵∠DAE=∠F,
∴∠AEB=∠F.
∴△ABE∽△ECF;
(2)∵△ABE∽△ECF,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴BC=AD=8.
∴EC=BCBE=82=6.
∴![]() .
.
∴FC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.
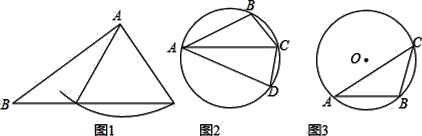
(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;
(2)如图3,△ABC内接于⊙O,⊙O的半径为![]() ,AB=6,∠BAC=30°,求AC的长;
,AB=6,∠BAC=30°,求AC的长;
(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
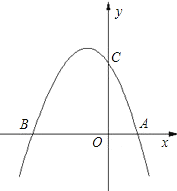
(1)求抛物线的解析式;
(2)若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求
,求![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标.
点的坐标.
(3)在抛物线上是否存在点![]() 使得
使得![]() 为等腰三角形?若存在,请求出一共有几个符合条件的点
为等腰三角形?若存在,请求出一共有几个符合条件的点![]() (简要说明理由)并写出其中一个点的坐标;若不存在这样的点
(简要说明理由)并写出其中一个点的坐标;若不存在这样的点![]() ,请简要说明理由.
,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
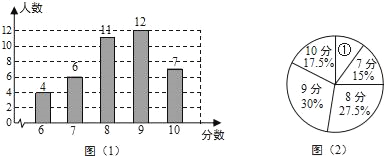
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的方程:
的方程:![]() ①和关于
①和关于![]() 的一元二次方程:
的一元二次方程:![]() ②(
②(![]() 、
、![]() 、
、![]() 均为实数),方程①的解为非正数.
均为实数),方程①的解为非正数.
(1)求![]() 的取值范围.
的取值范围.
(2)如果方程②的解为负整数,![]() ,
,![]() 且
且![]() 为整数,求整数
为整数,求整数![]() 的值.
的值.
(3)当方程②有两个实数根![]() 、
、![]() ,满足
,满足![]() ,且
,且![]() 为正整数,试判断
为正整数,试判断![]() 是否成立?请说明理由.
是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2a﹣1)x+a2+2=0有两个不相等的实数根.
(1)求实数a的取值范围,并求a的最大整数;
(2)x=1可能是方程的一个根吗?若是,请求出它的另一个根,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
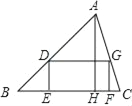
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com