
【题目】阅读理解:求代数式x2+4x+8的最小值.
解:因为x2+4x+8=(x2+4x+4)+4=(x+2)2+4≥4,所以当x=﹣2时,代数式x2+4x+8有最小值,最小值是4.仿照上述解题过程求值.
(1)应用:求代数式m2+2m+3的最小值.
(2)拓展:求代数式﹣m2+3m+![]() 的最大值.
的最大值.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.
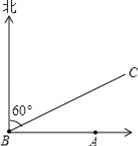
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式,例如:![]() ,
,![]() ,
,![]() ,…含有两个字母
,…含有两个字母![]() ,
,![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等对称式都可以用
等对称式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
请根据以上材料解决下列问题:
(1)式子:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,属于对称式的是 (填序号)
中,属于对称式的是 (填序号)
(2)已知![]() .
.
①若![]() ,求对称式
,求对称式![]() 的值
的值
②若![]() ,求对称式
,求对称式![]() 的最大值
的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,过B点作BE⊥AD,
中,过B点作BE⊥AD,![]() .
.
(1)如图1,点![]() 在
在![]() 的延长线上,连
的延长线上,连![]() ,作
,作![]() 于
于![]() ,交
,交![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 上,连
上,连![]() ,过
,过![]() 作
作![]() ,且
,且![]() ,连
,连![]() 交
交![]() 于
于![]() ,连
,连![]() ,问
,问![]() 与
与![]() 有何数量关系,并加以证明;
有何数量关系,并加以证明;
(3)如图3,点![]() 在CB延长线上,
在CB延长线上,![]() 且
且![]() ,连接
,连接![]() 、
、![]() 的延长线交
的延长线交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,则∠DAE= .
(2)若∠B=60°,∠C=20°,则∠DAE= .
(3)由(1)(2)猜想∠DAE与∠B,∠C之间的关系为 ,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.

(2)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
①找出图中与![]() 相等的线段,并加以证明;
相等的线段,并加以证明;
②求![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(﹣2,﹣1),试确定平移的方向和平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com