
【题目】在正方形![]() 中,动点
中,动点![]() 分别从
分别从![]() 两点同时出发,以相同的速度在直线
两点同时出发,以相同的速度在直线![]() 上移动;
上移动;
(1)如图①,当![]() 分别移动到边
分别移动到边![]() 的延长线上时,连接
的延长线上时,连接![]() 和
和![]() 与
与![]() 的关系为____ ;
的关系为____ ;

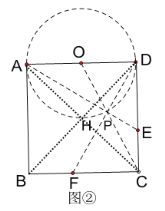
(2)如图②,己知正方形的边长为![]() 点
点![]() 和
和![]() 分别从点
分别从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 方向向终点
方向向终点![]() 和
和![]() 运动,连接
运动,连接![]() 和
和![]() ,交于点
,交于点![]() ,请你画出点
,请你画出点![]() 运动路线的草图,试求出线段
运动路线的草图,试求出线段![]() 的最小值.
的最小值.

(3)如图③,在(2)的条件下,求![]() 周长的最大值;
周长的最大值;

【答案】(1)AE=DF,AE⊥DF;(2)点![]() 运动路线见解析;线段CP的最小值为
运动路线见解析;线段CP的最小值为![]() ;(3)△APD周长的最大值为
;(3)△APD周长的最大值为![]() .
.
【解析】
(1)根据正方形的性质利用SAS证明△ADE≌△DCF,可得AE=DF,∠DAE=∠CDF,延长FD交AE于点G,求出∠ADG+∠DAE=90°即可;
(2)根据AE⊥DF可知点P在以AD为直径的![]() 圆弧上,当O、C、P三点共线时,线段CP最小,求出OC即可得到线段CP的最小值;
圆弧上,当O、C、P三点共线时,线段CP最小,求出OC即可得到线段CP的最小值;
(3)如图③,以AD为斜边向外作等腰直角△ADG,过点G作GM⊥AE于M,GN⊥FD交FD的延长线于点N,连接GP,首先证明△AMG≌△DNG,四边形GMPN是正方形,然后求出PA+PD=2GM,且GM的最大值=AG=![]() ,再由三角形周长公式可得答案.
,再由三角形周长公式可得答案.
解:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠DCF=90°,
∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,
∴DE=CF,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
延长FD交AE于点G,如图①所示,则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,
∴∠AGD=90°,
∴AE⊥DF,
故答案为:AE=DF,AE⊥DF;

(2)由(1)可知AE⊥DF,
∴在点E、F的运动过程中,∠APD始终是90°,
∴点P在以AD为直径的![]() 圆弧上,即劣弧DH,如图所示,
圆弧上,即劣弧DH,如图所示,
设圆心为O,连接OC,则O、C、P三点共线时,线段CP最小,
∵圆心O为AD中点,正方形的边长为4,
∴OA=OD=OP=2,
∴OC=![]() ,
,
∴线段CP的最小值为:![]() ;
;
(3)如图③,以AD为斜边向外作等腰直角△ADG,过点G作GM⊥AE于M,GN⊥FD交FD的延长线于点N,连接GP,
∵∠GMP=∠MPN=∠N=90°,
∴四边形GMPN是矩形,
∴∠MGN=∠AGD=90°,
∴∠AGM=∠DGN,
∵∠AMG=∠DNG=90°,AG=DG,
∴△AMG≌△DNG(AAS),
∴AM=DN,MG=NG,
∴矩形GMPN是正方形,
∴PA+PD=PM+AM+PN-DN=PM+PN=2PM=2GM,
∵GM≤AG,
∴GM的最大值=AG=![]() ,
,
∴PA+PD的最大值为![]() ,
,
∴△APD周长的最大值为:![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(﹣2,1),B(﹣1,4).
(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向上平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DBC的面积等于3,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,某市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如折线图,

请根据图像回答下列问题;
(1)当用电量是180千瓦时时,电费是_______________元;
(2)第二档的用电量范围是________________________;
(3)“基本电价”是__________________元/千瓦时;
(4)小明家4月份的电费是337.5元,这个月他用电__________________千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )

A. 5≤a≤12B. 12≤a≤3![]()
C. 12≤a≤4![]() D. 12≤a≤13
D. 12≤a≤13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.

(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为 ![]() .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com