
【题目】在直角坐标系![]() 中,已知点P是反比例函数
中,已知点P是反比例函数![]() (
(![]() >0)图象上一个动点,以P为圆心的圆始终与
>0)图象上一个动点,以P为圆心的圆始终与![]() 轴相切,设切点为A.
轴相切,设切点为A.
(1)如图1,⊙P运动到与![]() 轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
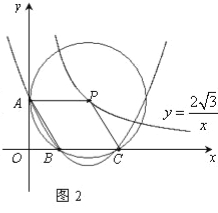
(2)如图2,⊙P运动到与![]() 轴相交,设交点为B,C.当四边形ABCP是菱形时:
轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的![]() .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.

【答案】(1)、正方形;(2)、①、A(0,![]() ),B(1,0)C(3,0);②、(0,
),B(1,0)C(3,0);②、(0,![]() ),(3,0),(4,
),(3,0),(4,![]() ),(7,8
),(7,8![]() ).
).
【解析】
试题分析:(1)、根据圆与坐标轴相等得出∠PAO=∠OKP=90°,又因为∠AOK=90°则得出四边形OKPA是矩形,根据OA=OK得出正方形;(2)、①、连接PB,设点P的横坐标为x,则纵坐标为![]() ,根据四边形为菱形得出△PBC为正三角形,得出PB=PA=x,PG=
,根据四边形为菱形得出△PBC为正三角形,得出PB=PA=x,PG=![]() ,根据sin∠PBG的值得出x的值,从而得到PG、PA、BC的值,得出A、B、C三点的坐标;②、根据三点坐标求出二次函数的解析式,然后求出直线BP的解析式,列出方程求出点M的坐标.
,根据sin∠PBG的值得出x的值,从而得到PG、PA、BC的值,得出A、B、C三点的坐标;②、根据三点坐标求出二次函数的解析式,然后求出直线BP的解析式,列出方程求出点M的坐标.
试题解析:(1)、四边形OKPA是正方形.
∵⊙P分别与两坐标轴相切,∴PA⊥OA,PK⊥OK.∴∠PAO=∠OKP=90°. 又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.∴四边形OKPA是矩形.又∵OA=OK,∴四边形OKPA是正方形.
(2)、①、连接PB,设点P的横坐标为x,则其纵坐标为![]() .过点P作PG⊥BC于G.
.过点P作PG⊥BC于G.
∵四边形ABCP为菱形,∴BC=PA=PB=PC.∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=![]() .sin∠PBG=
.sin∠PBG=![]() ,即
,即![]() .
.
解之得:x=±2(负值舍去).∴PG=![]() ,PA=BC=2.
,PA=BC=2.
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,∴OB=OG﹣BG=1,OC=OG+GC=3.
∴A(0,![]() ),B(1,0)C(3,0).
),B(1,0)C(3,0).
设二次函数解析式为:y=ax2+bx+c.据题意得: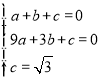
解之得:a=![]() ,b=-
,b=-![]() ,c=
,c=![]() .
.
∴二次函数关系式为:![]() .
.
②、设直线BP的解析式为:y=ux+v,据题意得: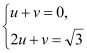
解之得:u=![]() ,v=-3
,v=-3![]() .∴直线BP的解析式为:
.∴直线BP的解析式为:![]() .
.
过点A作直线AM∥PB,则可得直线AM的解析式为:y=![]() x+
x+![]() .
.
解方程组: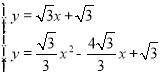 得:
得: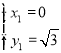 ;
;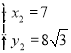 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为:y=![]() x+t.
x+t.
∴0=3![]() +t.∴t=-3
+t.∴t=-3![]() .∴直线CM的解析式为:y=
.∴直线CM的解析式为:y=![]() x-3
x-3![]() .
.
解方程组: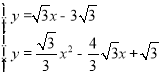 得:
得:![]() ;
;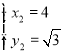 .
.
综上可知,满足条件的M的坐标有四个,
分别为:(0,![]() ),(3,0),(4,
),(3,0),(4,![]() ),(7,8
),(7,8![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
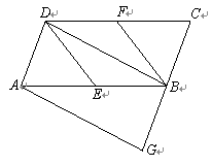
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在某分期比赛中有A、B、C三组家庭进行比赛:
(1)选手选择A组家庭的宝宝,直接写出在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通求选手至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣6x+5用配方法化成y=(x﹣h)2+k的形式,下列结果中正确的是( )
A.y=(x﹣6)2+5
B.y=(x﹣3)2+5
C.y=(x﹣3)2﹣4
D.y=(x+3)2﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
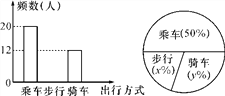
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com