
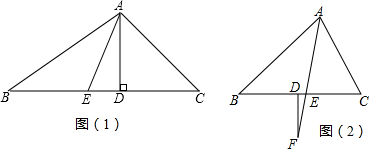
分析 (1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=$\frac{1}{2}$∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
(2)根据题意可知∠B=x°,∠C=(x+36)°,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC的度数,再根据FD⊥BC,可得出∠F的度数.
解答 解:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AD是△ABC角平分线,
∴∠CAE=$\frac{1}{2}$∠CAB=50°,
∵AE分别是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°;
(2)①∵∠B=x°,∠C=(x+36)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=$\frac{1}{2}×$[180°-x°-(x+36)°]=72°-x°,
②∠AEC=∠BAE+∠B=72°,
∵FD⊥BC,
∴∠F=18°.
点评 本题考查的是三角形的角平分线、中线和高以及三角形内角和定理,掌握三角形的角平分线、中线和高的概念,正确运用数形结合思想是解题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
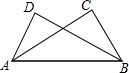 如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )| A. | 60° | B. | 35° | C. | 85° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
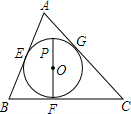 如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
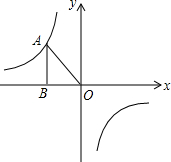 已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.
已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com