
【题目】观察下列各式:22﹣1=1×3,32﹣1=2×4,42﹣1=3×5,52﹣1=4×6,…,根据上述规律,第n个等式应表示为 .
科目:初中数学 来源: 题型:
【题目】列方程解应用题 某商店用2000元购进一批小学生书包,出售后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了2元,结果购买第二批书包用了6600元.
(1)请求出第一批每只书包的进价;
(2)该商店第一批和第二批分别购进了多少只书包;
(3)若商店销售这两批书包时,每个售价都是30元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要反映我区12月11日至17日这一周每天的最高气温的变化趋势,宜采用( )
A. 条形统计图 B. 折线统计图
C. 扇形统计图 D. 频数分布统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。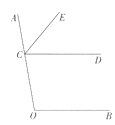
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE= , ∠COF= ![]() ∠COB。
∠COB。
(理由: )
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠。
(理由: )
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB. 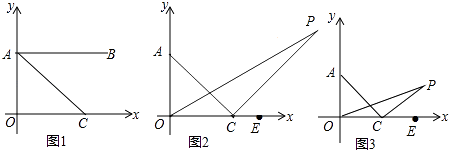
(1)求证:∠OAC=∠OCA;
(2)如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图3,在(2)中,若射线OP、OC满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( ) 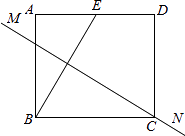
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com