
【题目】如图1,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB. 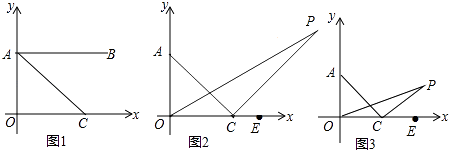
(1)求证:∠OAC=∠OCA;
(2)如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图3,在(2)中,若射线OP、OC满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
【答案】
(1)解:∵A(0,1),B(4,1),
∴AB∥CO,
∴∠OAB=90°,
∵AC平分∠OAB.
∴∠OAC=45°,
∴∠OCA=90°﹣45°=45°,
∴∠OAC=∠OCA;
(2)解:∵∠POC= ![]() ∠AOC,∴∠POC=
∠AOC,∴∠POC= ![]() ×90°=30°,
×90°=30°,
∵∠PCE= ![]() ∠ACE,∴∠PCE=
∠ACE,∴∠PCE= ![]() (180°﹣45°)=45°,
(180°﹣45°)=45°,
∵∠P+∠POC=∠PCE,
∴∠P=∠PCE﹣∠POC=15°
(3)解:∵∠POC= ![]() ∠AOC,∴∠POC=
∠AOC,∴∠POC= ![]() ×90°=
×90°= ![]() °,
°,
∵∠PCE= ![]() ∠ACE,∴∠PCE=
∠ACE,∴∠PCE= ![]() (180°﹣45°)=
(180°﹣45°)= ![]() °,
°,
∵∠P+∠POC=∠PCE,
∴∠P=∠PCE﹣∠POC= ![]() °
°
【解析】(1)根据AB坐标可以求得∠OAB大小,根据角平分线性质可求得∠OAC大小,即可解题;(2)根据题干中给出的∠POC= ![]() ∠AOC、∠PCE=
∠AOC、∠PCE= ![]() ∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题;(3)解法和(2)相同,根据题干中给出的∠POC=
∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题;(3)解法和(2)相同,根据题干中给出的∠POC= ![]() ∠AOC、∠PCE=
∠AOC、∠PCE= ![]() ∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题.
∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA= , PC=;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】式子7-3-4+18-11=(7+18)+(-3-4-11)是应用了( )
A. 加法交换律 B. 加法结合律
C. 分配律 D. 加法的交换律与结合律
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB2C2;.
查看答案和解析>>
科目:初中数学 来源: 题型:
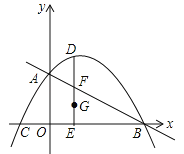
【题目】如图,抛物线![]() 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com