
����Ŀ����ͼ��������![]() �������ύ��A��B��C���㣬����B��4��0����C����2��0��������AB��AC���ڵ�һ�����ڵ�����������һ����D����D��DE��x�ᣬ����ΪE����AB�ڵ�F��
�������ύ��A��B��C���㣬����B��4��0����C����2��0��������AB��AC���ڵ�һ�����ڵ�����������һ����D����D��DE��x�ᣬ����ΪE����AB�ڵ�F��
��1����������ߵĽ���ʽ��
��2����DE������G��ʹG����D�����F��Գƣ���GΪԲ�ģ�GDΪ�뾶��Բ������G������һ������������ʱ����G��ĺ����ꣻ
��3����D����ֱ��DH��AC��AB��H������DHF��������ʱ���������ߺ�ֱ��AB�Ϸֱ�ȡM��N���㣬��ʹD��H��M��N�ĵ����ƽ���ı��Σ�����ֱ��д������Ҫ���M��N����ĺ����꣮
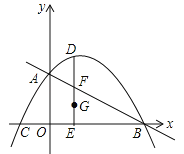
���𰸡���1��![]() ����2��2��
����2��2��![]() ����3��M��ĺ�����Ϊ
����3��M��ĺ�����Ϊ![]() ��N��ĺ�����Ϊ
��N��ĺ�����Ϊ![]() ��
��
��������
�����������1������B��C�������������ϣ����������ߵõ������飬���a��b��ֵ���ɣ�
��2��ֱ��AB�Ľ���ʽΪ![]() ����F�������Ϊ��x��
����F���������x��![]() ������D���������x��
������D�������Ϊ��x��![]() ��������G����D�����F��Գƣ�����G�������Ϊ��x��
��������G����D�����F��Գƣ�����G�������Ϊ��x��![]() ��������GΪԲ�ģ�GDΪ�뾶��Բ��ʹ����G������һ�����������У�������������������������G��x�������������DG=GE��������G��y�������������DG=OE��
��������GΪԲ�ģ�GDΪ�뾶��Բ��ʹ����G������һ�����������У�������������������������G��x�������������DG=GE��������G��y�������������DG=OE��
��3��M��ĺ�����Ϊ![]() ��N��ĺ�����Ϊ
��N��ĺ�����Ϊ![]() ��
��
�����������1����B��C������������![]() �ϣ���
�ϣ���![]() ����ã�
����ã�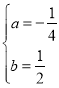 ��
��
���������������![]() ��
��
��2��������![]() �����A������Ϊ��0��2������ֱ��AB�Ľ���ʽΪ
�����A������Ϊ��0��2������ֱ��AB�Ľ���ʽΪ![]() ����
����![]() ����ã�
����ã� ����ֱ��AB�Ľ���ʽΪ
����ֱ��AB�Ľ���ʽΪ![]() ����F�������Ϊ��x��
����F���������x��![]() ������D���������x��
������D�������Ϊ��x��![]() ������G����D�����F��Գƣ���G�������Ϊ��x��
������G����D�����F��Գƣ���G�������Ϊ��x��![]() ��������GΪԲ�ģ�GDΪ�뾶��Բ��ʹ����G������һ�����������У�
��������GΪԲ�ģ�GDΪ�뾶��Բ��ʹ����G������һ�����������У�
������G��x�������������DG=GE����![]() =
=![]() ������
������![]() ����ã�
����ã�![]() ��
��![]() ����ȥ����
����ȥ����
������G��y�������������DG=OE����![]() ����ã�
����ã�![]() ��
��![]() ����ȥ����
����ȥ����
���ϣ���GΪԲ�ģ�GDΪ�뾶��Բ������G������һ������������ʱ��G��ĺ�����Ϊ2��![]() ��
��
��3��M��ĺ�����Ϊ![]() ��N��ĺ�����Ϊ
��N��ĺ�����Ϊ![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�A��0��1����B��4��1����CΪx����������һ�㣬��ACƽ�֡�OAB�� 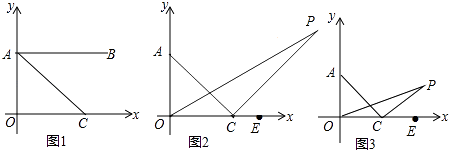
��1����֤����OAC=��OCA��
��2����ͼ2�����ֱ�����AOC�����ȷ�����OCA����ǵ����ȷ��߽��ڵ�P���������POC= ![]() ��AOC����PCE=
��AOC����PCE= ![]() ��ACE�����P�Ĵ�С��
��ACE�����P�Ĵ�С��
��3����ͼ3���ڣ�2���У�������OP��OC�����POC= ![]() ��AOC����PCE=
��AOC����PCE= ![]() ��ACE�������OPC�Ĵ�С����֤����Ľ��ۣ��ú�n��ʽ�ӱ�ʾ��
��ACE�������OPC�Ĵ�С����֤����Ľ��ۣ��ú�n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д��ʡ�ԼӺź͵���ʽ��Ϊ-6-7-2+9��ʽ���ǣ� ��
A. ��-6��-��+7��-��-2��+��+9�� B. -��+6��-��-7��-��+2��-��+9��
C. ��-6��+��-7��+��+2��-��-9�� D. -6-��+7��+��-2��-��-9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B���߶�AC�ϣ���BC=2AB��D��E�ֱ���AB��BC���е㣮�����н��ۣ���AB= ![]() AC����B��AE���е㣻��EC=2BD����DE=AB��������ȷ���У� ��
AC����B��AE���е㣻��EC=2BD����DE=AB��������ȷ���У� �� ![]()
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У���E��AD���е㣬��AE=1��BE�Ĵ�ֱƽ����MNǡ�ù���C������ε�һ��AB�ij���Ϊ�� �� 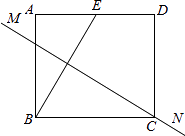
A.1
B.![]()
C.![]()
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij��ѧ��չ����Ϊ���Ұ��Ķ�����ר��������˽�ѧУ1200��ѧ��һ�����Ķ��鼮�������������ȡ����ѧ������ͳ�ƣ����Ƴ�������δ��ɵ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���������������⣺
���� | Ƶ�� | Ƶ�� |
0��x��5 | 4 | 0.08 |
5��x��10 | 14 | 0.28 |
10��x��15 | 16 | a |
15��x��20 | b | c |
20��x��25 | 10 | 0.2 |
�ϼ� | d | 1.00 |
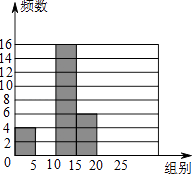
��1��a= �� b= �� c= �� d= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����ݸ����������Ƹ�Уѧ���Ķ��鼮������15�������ϵ�������
��4������Ķ��鼮������10�������ϵ�����ռ��������70%���ϣ���ô��У����Ϊ������У����������������ݷ�����У�Ƿ��ܻ�ô���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
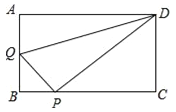
����Ŀ���ھ���ABCD�У�AB=3��AD=4������Q�ӵ�A��������ÿ��1����λ���ٶȣ���AB���B�ƶ���ͬʱ��P�ӵ�B����������ÿ��1����λ���ٶȣ���BC���C�ƶ�������QP��QD��PD����������ͬʱ�˶���ʱ��Ϊx�루0��x��3��������������⣺
��1�����QPD�����ΪS���ú�x�ĺ�����ϵʽ��ʾS����xΪ��ֵʱ��S�����ֵ���������Сֵ��
��2���Ƿ����x��ֵ��ʹ��QP��DP����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
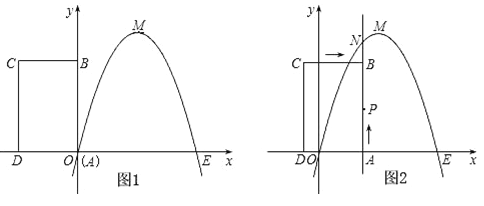
����Ŀ����ͼ����֪�����߾�������ԭ��O��x������һ��E������M������Ϊ��2��4��������ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
��1���������������Ӧ�ĺ�����ϵʽ��
��2��������ABCD��ÿ��1����λ���ȵ��ٶȴ���ͼ��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��3����ֱ��AB��������ߵĽ���ΪN����ͼ2��ʾ����
�ٵ�t=![]() ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
������P��N��C��DΪ����Ķ�������ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
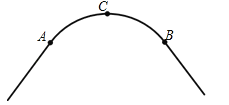
����Ŀ����ͼ��һ����·��ת�䴦��һ��Բ����![]() ����
����
��1����ֱ�ߺ�Բ������![]() ����Բ��Բ��O����Ҫ������ͼ�ۼ�����д������
����Բ��Բ��O����Ҫ������ͼ�ۼ�����д������
��2����![]() ���е�C����AB�ľ���Ϊ20m��AB=80m����
���е�C����AB�ľ���Ϊ20m��AB=80m����![]() ����Բ�İ뾶��
����Բ�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com