
【题目】广州市某中学开展主题为“我爱阅读”的专题调查活动,了解学校1200名学生一年内阅读书籍的数量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
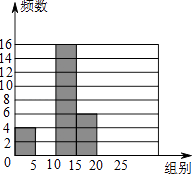
(1)a= , b= , c= , d= .
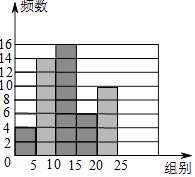
(2)补全频数分布直方图.
(3)根据该样本,估计该校学生阅读书籍数量在15本或以上的人数.
(4)如果阅读书籍数量在10本或以上的人数占总人数的70%以上,那么该校能评为“书香校园”,请根据上述数据分析该校是否能获得此荣誉,并说明理由.
【答案】
(1)0.32,6,0.12,50
(2)解:补全的频数分布直方图,如右图所示;
(3)解:由题意可得,
该校学生阅读书籍数量在15本或以上的有:1200×(0.12+0.2)=384(人),
答:该校学生阅读书籍数量在15本或以上的有384人;
(4)解:该校不能获得“书香校园”此荣誉,
理由:∵(50﹣4﹣14)÷50=64%<70%,
∴该校不能获得“书香校园”此荣誉.
【解析】解:(1)根据题意可的,
a=(16÷4)×0.08=0.32,b=6,c=(6÷4)×0.08=0.12,d=4÷0.08=50,
(2)补全的频数分布直方图,如右图所示;

(3)由题意可得,
该校学生阅读书籍数量在15本或以上的有:1200×(0.12+0.2)=384(人),
答:该校学生阅读书籍数量在15本或以上的有384人;
(4)该校不能获得“书香校园”此荣誉,
理由:∵(50﹣4﹣14)÷50=64%<70%,
∴该校不能获得“书香校园”此荣誉.
所以答案是:(1)0.32,6,0.12,50;(2)图见解答;(3)该校学生阅读书籍数量在15本或以上的有384人;(4)不能获得“书香校园”此荣誉.
【考点精析】关于本题考查的频数分布直方图,需要了解特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能得出正确答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,
的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .其中正确的结论是 (填入正确结论的序号).
.其中正确的结论是 (填入正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
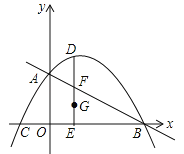
【题目】如图,抛物线![]() 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李到农贸批发市场了解到苹果和西瓜的价格信息如下:
水果品种 | 苹果 | 西瓜 |
批发价格 | 8元/公斤 | 1.6元/公斤 |
零售价格 | 10元/公斤 | 2元/公斤 |
他共用280元批发了苹果和西瓜共75公斤,
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
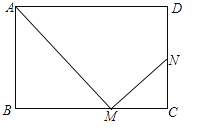
【题目】在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com