
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA= , PC=;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. 
【答案】
(1)t;34﹣t
(2)解:当P点在Q点右侧,且Q点还没有追上P点时,
3t+2=14+t
解得:t=6,
∴此时点P表示的数为﹣4,
当P点在Q点左侧,且Q点追上P点后,相距2个单位,
3t﹣2=14+t解得:t=8,
∴此时点P表示的数为﹣2,
当Q点到达C点后,当P点在Q点左侧时,
14+t+2+3t﹣34=34
解得:t=13,
∴此时点P表示的数为3,
当Q点到达C点后,当P点在Q点右侧时,
14+t﹣2+3t﹣34=34
解得:t=14,
∴此时点P表示的数为4,
综上所述:点P表示的数为﹣4,﹣2,3,4
【解析】解:(1)∵动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒,
∴P到点A的距离为:PA=t,P到点C的距离为:PC=(24+10)﹣t=34﹣t;
所以答案是:t,34﹣t;
【考点精析】掌握数轴和两点间的距离是解答本题的根本,需要知道数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣![]() 的图象经过点C.
的图象经过点C.
(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.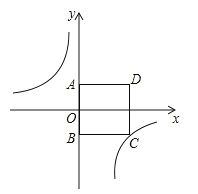
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线![]() 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要反映我区12月11日至17日这一周每天的最高气温的变化趋势,宜采用( )
A. 条形统计图 B. 折线统计图
C. 扇形统计图 D. 频数分布统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )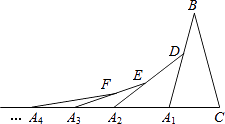
A.( ![]() )n75°
)n75°
B.( ![]() )n﹣165°
)n﹣165°
C.( ![]() )n﹣175°
)n﹣175°
D.( ![]() )n85°
)n85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB. 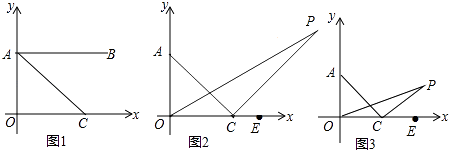
(1)求证:∠OAC=∠OCA;
(2)如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图3,在(2)中,若射线OP、OC满足∠POC= ![]() ∠AOC,∠PCE=
∠AOC,∠PCE= ![]() ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写成省略加号和的形式后为-6-7-2+9的式子是( )
A. (-6)-(+7)-(-2)+(+9) B. -(+6)-(-7)-(+2)-(+9)
C. (-6)+(-7)+(+2)-(-9) D. -6-(+7)+(-2)-(-9)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com