[题目]解方程:(1)7(2x–1)–3(4x–1)=4(3x+2)–1,(2). 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】解方程：（1）7（2x–1）–3（4x–1）=4（3x+2）–1；

（2）.

【答案】（1）x=﹣1.1；（2）x=4．

【解析】

（1）先去括号再移项即可，注意去括号时，括号前为负号时，括号内每项均要变号，移项也要变号；

（2）方程两边先同时乘以12去分母，再去括号和移项即可.

解：（1）去括号得：14x﹣7﹣12x+3=12x+8﹣1，

移项得：14x﹣12x﹣12x=8﹣1+7﹣3，

合并同类项得：﹣10x=11，

系数化为1得：x=﹣1.1，

（2）方程两边同时乘以12得：4（7x﹣1）﹣6（5x+1）=24﹣3（3x+2），

去括号得：28x﹣4﹣30x﹣6=24﹣9x﹣6，

移项得：28x﹣30x+9x=24﹣6+4+6，

合并同类项得：7x=28，

系数化为1得：x=4．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】从﹣2，﹣1，0，1，2这5个数中，随机抽取一个数记为a，则使关于x的不等式组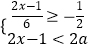有解，且使关于x的一元一次方程 +1= 的解为负数的概率为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，对于与坐标轴不平行的直线l和点P，给出如下定义：过点P作x轴，y轴的垂线，分别交直线l于点M，N，若PM+PN≤4，则称P为直线l的近距点，特别地，直线上l所有的点都是直线l的近距点．已知点A(-，0)，B(0，2)，C(-2，2)．

（1）当直线l的表达式为y=x时，

①在点A，B，C中，直线l的近距点是；

②若以OA为边的矩形OAEF上所有的点都是直线l的近距点，求点E的纵坐标n的取值范围；

（2）当直线l的表达式为y=kx时，若点C是直线l的近距点，直接写出k的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知抛物线y=ax2+bx+c的顶点为（1，0），且经过点（0，1）．
（1）求该抛物线对应的函数的解析式；
（2）将该抛物线向下平移m（m＞0）个单位，设得到的抛物线的顶点为A，与x轴的两个交点为B、C，若△ABC为等边三角形．
①求m的值；
②设点A关于x轴的对称点为点D，在抛物线上是否存在点P，使四边形CBDP为菱形？若存在，写出点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，四边形是矩形 ,是延长线上的一点，是上一点，;若,则 = ________ .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图的数阵是由77个偶数排成：

（1）如图中任意作一个平行四边形框，设左上角的数为x，那么其他3个数从小到大可分别表示为　　．

（2）小红说这4个数的和是292，能求出这4个数吗？若存在，请求出这4个数．不存在说明理由．

（3）小明说4个数的和是420，存在这样的数吗？若存在，请求出这4个数，不存在说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】计算：

（1）-16-（-1+）÷3×[2-（-4）2]

（2）解方程：-=-1

（3）先化简，再求值：2（x2-2xy）+[2y2-3（x2-2xy+y2）+x2]，其中x=1，y=-．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】一只小球落在数轴上的某点，第一次从向左跳1个单位到，第二次从向右跳2个单位到，第三次从向左跳3个单位到，第四次从向右跳4个单位到，若小球从原点出发，按以上规律跳了6次时，它落在数轴上的点所表示的数是__________；若小球按以上规律跳了2n次时，它落在数轴上的点所表示的数恰好是，则这只小球的初始位置点所表示的数是__________.