
【题目】如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是段AB的“2倍点”.
(1)线段的中点__________这条线段的“2倍点”;(填“是”或“不是”)
(2)若AB=15cm,点C是线段AB的“2倍点”.求AC的长;
(3)如图②,已知AB=20cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动.点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动.点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s),当t=_____________s时,点Q恰好是线段AP的“2倍点”.(请直接写出各案)
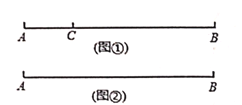
【答案】(1)是;(2)5cm或7.5cm或10cm;(3)10或![]() .
.
【解析】
(1)根据“2倍点”的定义即可求解;
(2)分点C在中点的左边,点C在中点,点C在中点的右边三种情况,进行讨论求解即可;
(3)根据题意画出图形,P应在Q的右边,分别表示出AQ、QP、PB,求出t的范围.然后根据(2)分三种情况讨论即可.
(1)∵整个线段的长是较短线段长度的2倍,∴线段的中点是这条线段的“2倍点”.
故答案为:是;
(2)∵AB=15cm,点C是线段AB的2倍点,∴AC=15![]() 5cm或AC=15
5cm或AC=15![]() 7.5cm或AC=15
7.5cm或AC=15![]() 10cm.
10cm.
(3)∵点Q是线段AP的“2倍点”,∴点Q在线段AP上.如图所示:
![]()
由题意得:AP=2t,BQ=t,∴AQ=20-t,QP=2t-(20-t)=3t-20,PB=20-2t.
∵PB=20-2t≥0,∴t≤10.
∵QP=3t-20≥0,∴t≥![]() ,∴
,∴![]() ≤t≤10.
≤t≤10.
分三种情况讨论:
①当AQ=![]() AP时,20-t=
AP时,20-t=![]() ×2t,解得:t=12>10,舍去;
×2t,解得:t=12>10,舍去;
②当AQ=![]() AP时,20-t=
AP时,20-t=![]() ×2t,解得:t=10;
×2t,解得:t=10;
③当AQ=![]() AP时,20-t=
AP时,20-t=![]() ×2t,解得:t
×2t,解得:t![]() ;
;
答:t为10或![]() 时,点 Q是线段AP的“2倍点”.
时,点 Q是线段AP的“2倍点”.


科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上. 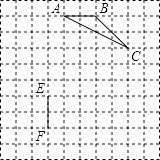
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
……
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与计算
(1)已知:![]() .
.
求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=![]() (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)

(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=∠B=30°,CD平分∠ACB,M、N分别是BC、AC的中点.图中等于60°的角有( )个.
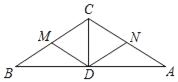
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系中的位置如图所示,其中A(﹣3,5),B(﹣5,2),C(﹣1,3),直线l经过点(0,1),并且与x轴平行,△A′B′C′与△ABC关于线1对称.
(1)画出△A′B′C′,并写出△A′B′C′三个顶点的坐标: ;
(2)观察图中对应点坐标之间的关系,写出点P(a,b)关于直线l的对称点P′的坐标: ;
(3)若直线l′经过点(0,m),并且与x轴平行,根据上面研究的经验,写出点Q(c,d)关于直线1′的对称点Q′的坐标: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上, ![]() =
= ![]() ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y= ![]() 的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于 ![]() ,则k的值是.
,则k的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
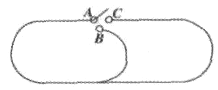
【题目】如图是一个玩具火车轨道,点A有个变轨开关,可以连接点B或点C.小圈轨道的周长是2米,大圈轨道的周长是4米.开始时,点A连接点C,火车从点A出发,按照顺时针方向在轨道上移动,同时变轨开关每隔一分钟变换一次轨道连接.若火车的速度是每分钟10米,则火车第10次回到A点时用了 分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com