
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ-3��B��������λ�ڵ�A�Ҳ�һ�㣬��AB=12������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������B���������˶������˶�ʱ��Ϊt�룮
��1�������ϵ�B��ʾ����Ϊ______����P��ʾ����Ϊ______���ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������ÿ��1����λ���ȵ��ٶ����������A���������˶�����P����Qͬʱ����������P���Q�غϺ�P���ϸı䷽�����Q�������A���������˶�����P����Q���˶������У��ٶ�ʼ�ձ��ֲ��䣩������P����A��ʱ��P��Qֹͣ�˶������˶�ʱ��Ϊt�룮
�ٵ���P���Q�غ�ʱ����t��ֵ���������ʱ��P��ʾ������
�ڵ���P���߶�AQ�����ȷֵ�ʱ����t��ֵ��
![]()
���𰸡���1��9�� -3+2t����2���ٵ�t=4ʱ����P���Q�غϣ���ʱ��P��ʾ����Ϊ5���ڵ�t=![]() ���3���6���
���3���6���![]() ��ʱ����P���߶�AQ�����ȷֵ㣮
��ʱ����P���߶�AQ�����ȷֵ㣮
��������
��1�����������ľ������ɵã�
��2���ٸ����غ�ǰ���ߵ�·�̺͵���AB�ij����з������ɵã��ڷֵ�P���Q�غ�ǰ���غϺ����ݵ�P���߶�AQ�����ȷֵ��߶μ��������ϵ�����ݴ��г��������ɵã�
�⣺��1��������֪����B��ʾ������-3+12=9����P��ʾ������-3+2t��
�ʴ�Ϊ��9��-3+2t��
��2���ٸ������⣬�ã���1+2��t=12��
��ã�t=4��
��-3+2t=-3+2��4=5��
�𣺵�t=4ʱ����P���Q�غϣ���ʱ��P��ʾ����Ϊ5��
��P��Q�غ�ǰ��
��2AP=PQʱ����2t+4t+t=12�����t=![]() ��
��
��AP=2PQʱ����2t+t+t=12�����t=3��
P��Q�غϺ�
��AP=2PQʱ����2��8-t��=2��t-4�������t=6��
��2AP=PQʱ����4��8-t��=t-4�����t=![]() ��
��
������������t=![]() ���3���6���
���3���6���![]() ��ʱ����P���߶�AQ�����ȷֵ㣮
��ʱ����P���߶�AQ�����ȷֵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������н������ھ���������ѧУ����������ѧϰ�ա����涨ÿ����ѧУ�������κ���ʽ���ü�ͥ��ҵ��Ϊ�˽��ѧУ����ʵ��������ߡ����꼶ѧ���������ȡ�˲���ѧ���ķ��������������������Ŀ��ÿ��ֻ��ѡһ���A�������Ķ���B�������Ͷ���C������������D��ѧ��ѧϰ��E�����ʵ����F��������Ŀ���е��飬���ݵ����������������в�������ͳ��ͼ���������ͳ��ͼ����������⣺ 
��1���˴γ�����������Ϊ �� �벹ȫ����ͳ��ͼ��
��2��ȫ��Լ��4������У����ѧ�����Թ���ȫ��ѧ����ѡ����������������Լ�ж����ˣ�
��3�����꼶��1�����ѡ�����ʵ����2��Ů����1��������ѡ��2���μ�У�����ʵ�������������״ͼ���б������ǡ��ѡ��1��1Ů�ĸ����Ƕ��٣����оٳ����еȿ��ܵĽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B���ر���ɽ�������Ҫ��A�ص�B�أ�ֻ��������ͼ��ʾ�Ĺ�·�ȴ�A�ص�C�أ�����C�ص�B�أ��ּƻ���������A��B����ֱ�߹�ͨ���������ã���CAB=30�㣬��CBA=45�㣬AC=20km����������ͨ����������ͨǰ��ȣ���A�ص�B�ص�·�̽����̶��٣��������ȷ��0.1km���ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��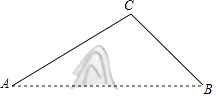
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�ڿ�ѧǰϦ������ij�ľߵ���4000Ԫ��������������ܿ����꣬��������4500Ԫ�����ڶ����������֪�ڶ��������������ֻ���ǵ�һ�������������ֻ����1.5������ÿֻ����Ľ��۱ȵ�һ���Ľ�����5Ԫ�����һ�����ÿֻ�Ľ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON��30�㣬��B1��B2��B3����A1��A2��A3���ֱ���OM��ON�ϣ��ҡ�A1B1A2����A2B2A3����A3B3A4�����ֱ�Ϊ�ȱ������Σ���֪OA1��1�����A2018B2018A2019�ı߳�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������⣺������ֱ�߱�������ֱ�����أ�ͬλ����ȣ���0.1������ƽ������0.01��������ƽ��������������������1���������P��3-2n��1������������ľ�����ȣ���n=1������a2=b2����a=b������![]() =
=![]() ����a=b�����м�����ĸ����ǣ�������
����a=b�����м�����ĸ����ǣ�������
A. 3��B. 4��C. 5��D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ͼ�٣���֪����A��������·BD�ľ���ΪAB��CΪ��·BD�ϵľƵ꣬�Ӻ���A���Ƶ�C���ȳ˴�����½��D������Ϊa���ٳ�����������Ϊ���ٵ�n������Dѡ�ںδ�ʱ������ʱ����̣�
��������������n=2����ʱ��t= ![]() +
+ ![]() ����aΪ��ֵʱ������ת��Ϊ����BC��ȷ��һ��D��ʹ��AD+
����aΪ��ֵʱ������ת��Ϊ����BC��ȷ��һ��D��ʹ��AD+ ![]() ��ֵ��С����ͼ�ڣ�����C������CM��ʹ�á�BCM=30�㣮
��ֵ��С����ͼ�ڣ�����C������CM��ʹ�á�BCM=30�㣮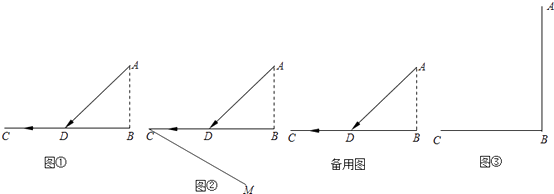
��1������D��DE��CM������ΪE����˵����DE= ![]() ��
��
��2����������������ͼ���л�������ʱ����̵ĵ�½��D�䣬��˵�����ɣ�
��3����ģ�����á�������ա������������е���ز��裬���ͼ���е����⣨д�����巽���������ͼ�γ��֡�ͼ���н����������������ͼ�ķ����ȣ���
��4����ͼ�ۣ�������һ��־A������BC�ľ���AB=300m��BC=300m������Ա��C�㴦���ֱ�־A��������ȣ�
����ǰȥӪ�ȣ�������Ա�ڰ����ܵ��ٶȶ���6m/s���ں�����Ӿ���ٶȶ���2m/s�������Ա��C�������
��A�������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��������ABCD�Ķ���B����A��C��ֱ��l�ľ���ֱ�Ϊ2��3����������ε����Ϊ(����)

A. 5 B. 6 C. 9 D. 13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���OABC�Ķ���A������Ϊ����4��0��������B�ڵڶ����ޣ���BAO=60�㣬BC��y���ڵ�D��DB��DC=3��1��������y= ![]() ��k��0��x��0����ͼ����C����k��ֵΪ�� ��
��k��0��x��0����ͼ����C����k��ֵΪ�� ��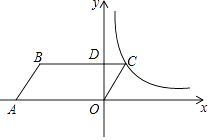
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com