
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F. 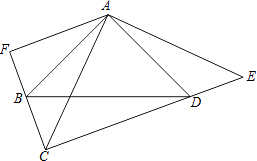
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF.
【答案】
(1)解:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中,
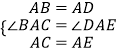 ,
,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD,
∴ ![]()
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF
(3)证明:过点A作AG⊥CG,垂足为点G,
∵AC平分∠ECF,AF⊥CB,
∴AF=AG,
又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
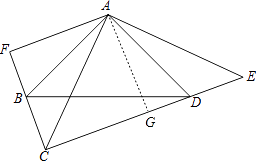
【解析】(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;(2)根据等腰直角三角形的性质得出∠ACE=∠AEC=45°,△ABC≌△ADE求出∠ACB=∠AEC=45°,推出∠ACB=∠ACE即可;(3)过点A作AG⊥CG,垂足为点G,求出AF=AG,求出CG=AG=GE,即可得出答案.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种纸一张的厚度约为0.0089cm,用科学记数法表示这个数为( )
A.8.9×10﹣5
B.8.9×10﹣4
C.8.9×10﹣3
D.8.9×10﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点构成的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对七年级男生进行引体向上测试,能做7个即达标,其中有8名男生的成绩分别为(单位:个)9,6,7,10,5,4,8,7.请你用正数或负数表示它们.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是我市四个景区今年2月份某天6时的气温,其中气温最低的景区是( )
景区 | 潜山公园 | 陆水湖 | 隐水洞 | 三湖连江 |
气温 | ﹣1℃ | 0℃ | ﹣2℃ | 2℃ |
A.潜山公园
B.陆水湖
C.隐水洞
D.三湖连江
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( ) 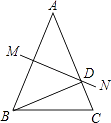
A.20°
B.30°
C.40°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B. 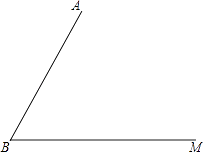
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①在射线BM上作一点C,使AC=AB;
②作∠ABM的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com