Question

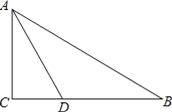
【题目】已知：如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．

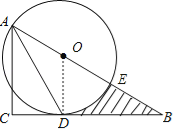
（1）以AB边上一点O为圆心，过A、D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；

（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=2，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和π）

Answer 1

【答案】（1）作图见解析；直线BC与⊙O的位置关系为相切，理由见解析；（2）线段BD、BE与劣弧DE所围成的图形面积为2﹣π．

【解析】试题分析：（1）根据题意得：O点应该是AD垂直平分线与AB的交点；由∠BAC的角平分线AD交BC边于D，与圆的性质可证得AC∥OD，又由∠C=90°，则问题得证；

（2）设⊙O的半径为r．则在Rt△OBD中，利用勾股定理列出关于r的方程，通过解方程即可求得r的值；然后根据扇形面积公式和三角形面积的计算可以求得“线段BD、BE与劣弧DE所围成的图形面积为：S△ODB﹣S扇形ODE=2﹣π”．

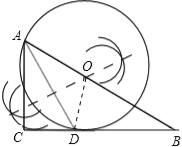
解：（1）如图：连接OD，

∵OA=OD，

∴∠OAD=∠ADO，

∵∠BAC的角平分线AD交BC边于D，

∴∠CAD=∠OAD，

∴∠CAD=∠ADO，

∴AC∥OD，

∵∠C=90°，

∴∠ODB=90°，

∴OD⊥BC，

即直线BC与⊙O的切线，

∴直线BC与⊙O的位置关系为相切；

（2）设⊙O的半径为r，则OB=6﹣r，又BD=2，

在Rt△OBD中，

OD2+BD2=OB2，

即r2+（2）2=（6﹣r）2，

解得r=2，OB=6﹣r=4，

∴∠DOB=60°，

∴S扇形ODE==π，

S△ODB=OD×BD=×2×2=2，

∴线段BD、BE与劣弧DE所围成的图形面积为：S△ODB﹣S扇形ODE=2﹣π．