
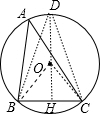
 如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).
如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
 某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.
某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.| 类型 | 两红 | 一红一黄 | 一红一蓝 | 一黄一蓝 |
| 价值 | 200元 | 150元 | 100元 | 50元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、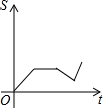 |
B、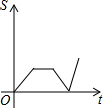 |
C、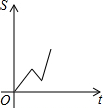 |
D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
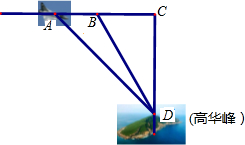 钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值:
钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值:| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com