
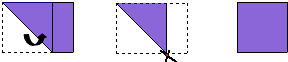
 情景再现
情景再现分析 操作探究(1)根据操作的方法可得a=2;
(2)当一个可裁长方形只经过两次裁剪就可以得到全部正方形,则所有符合条件的a的值为3个1或1为2个(a-1);
(3)结合(1)、(2)题作出图形;
方法迁移(1)利用列举法,尝试最小的几个非0自然数,再结合“自然数5.最少经过5步运算可得1”,即可得出结论;
(2)首先根据题意,应用逆推法,用1乘以2,得到2;用2乘以2,得到4;用4乘以2,得到8;用8乘以2,得到16;然后分类讨论,判断出所有符合条件的m的值为多少即可.
解答 解:操作探究:
(1)当一个可裁长方形只经过一次裁剪就可以得到全部正方形,则a的值为2个1,
故答案为:2;
(2)当一个可裁长方形只经过两次裁剪就可以得到全部正方形,则所有符合条件的a的值为3个1或1为2个(a-1),
故答案为:1.5或3;
(3)当一个可裁长方形只经过三次裁剪就可以得到全部正方形,画出符合条件可裁长方形如图: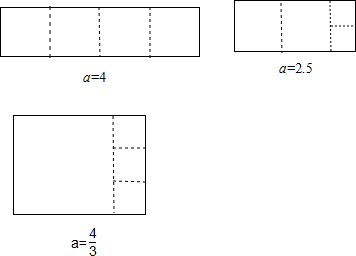
方法迁移:
(1)12$\stackrel{÷2}{→}$6$\stackrel{÷2}{→}$3$\stackrel{×3+1}{→}$10$\stackrel{÷2}{→}$5$\stackrel{×3+1}{→}$16$\stackrel{÷2}{→}$8$\stackrel{÷2}{→}$4$\stackrel{÷2}{→}$2$\stackrel{÷2}{→}$1,
自然数12最少经过9步运算可得到1,
故答案为:9;
(2)根据分析,可得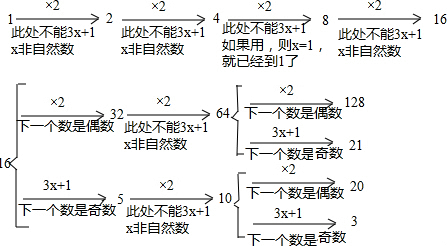
则所有符合条件的m的值为:128、21、20、3.
故答案为:128、21、20、3.
点评 (1)此题主要考查了探寻数列规律问题,考查了逆推法的应用,注意观察总结出规律,并能正确的应用规律.
(2)此题还考查了推理和论证问题,要熟练掌握,解答此题的关键是要明确:①演绎推理是从一般规律出发,运用逻辑证明或数学运算,得出特殊事实应遵循的规律,即从一般到特殊.②归纳推理就是从许多个别的事物中概括出一般性概念、原则或结论,即从特殊到一般.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
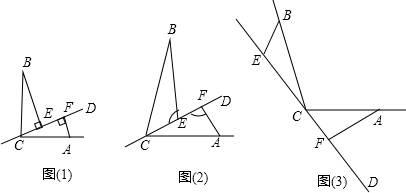
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
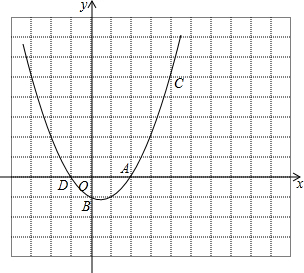
 如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.
如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
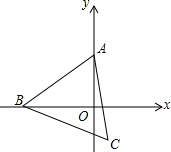 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.
如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
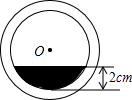 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com