
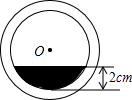
 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2. 分析 作OD⊥AB于C,交小⊙O于D,则CD=2,由垂径定理可知AC=CB,利用正弦函数求得∠OAC=30°,进而求得∠AOC=120°,利用勾股定理即可求出AB的值,从而利用S扇形-S△AOB求得杯底有水部分的面积.
解答 解:作OD⊥AB于C,交小⊙O于D,则CD=2,AC=BC,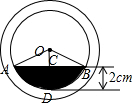
∵OA=OD=4,CD=2,
∴OC=2,
在RT△AOC中,sin∠OAC=$\frac{OC}{OA}$=$\frac{1}{2}$,
∴∠OAC=30°,
∴∠AOB=120°,
AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=2$\sqrt{3}$,
∴AB=4$\sqrt{3}$,
∴杯底有水部分的面积=S扇形-S△AOB=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=($\frac{16}{3}$π-4$\sqrt{3}$)cm2
故答案为($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 情景再现
情景再现查看答案和解析>>
科目:初中数学 来源: 题型:解答题
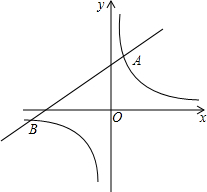 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com