
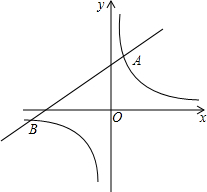
 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).分析 (1)将A点坐标代入反比例函数y=$\frac{m}{x}$,求出m的值,从而得到反比例函数解析式,将B(n,-2)代入反比例函数解析式,求出n的值,然后将A、B两点坐标代入即可求出一次函数解析式.
(2)由图象可直接观察出一次函数的值小于反比比例函数的值时x的取值范围.
解答 解:(1)将A(1,4)代入反比例函数y=$\frac{m}{x}$得,m=4,
则反比例函数解析式为y=$\frac{4}{x}$;
将B(n,-2)代入反比例函数解析式y=$\frac{4}{x}$得,
-2=$\frac{4}{x}$,n=-2,
B点坐标为(-2,-2).
设一次函数解析式为y=kx+b,
将A(1,4),B(-2,-2)分别代入解析式得,
$\left\{\begin{array}{l}{k+b=4}\\{-2k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$.
故一次函数解析式为y=2x+2.
(2)当一次函数的值小于反比例函数的值时,x的取值范围是x<-2或0<x<1.
点评 本题考查了反比例函数与一次函数的交点问题及待定系数法求函数解析式,要注意结合图形的性质并挖掘图形提供的隐含条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
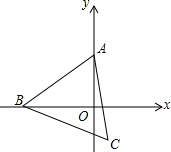 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.
如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
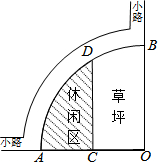 如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积.
如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
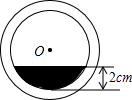 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
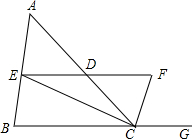 如图,CE,CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D.
如图,CE,CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com