
 如图,线段AC是矩形ABCD的对角线,
如图,线段AC是矩形ABCD的对角线,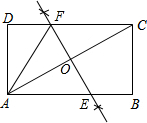 (1)解:如图:分别以A,C为圆心,以大于AC的长为半径画弧,然后连接即可;
(1)解:如图:分别以A,C为圆心,以大于AC的长为半径画弧,然后连接即可;
|


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
| 4 |
| a2+b2 |
| a-1 |
| x2+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
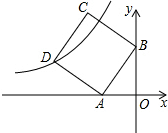 如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=
如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=| k |
| x |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
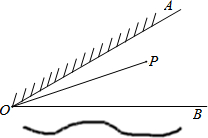 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.查看答案和解析>>
科目:初中数学 来源: 题型:
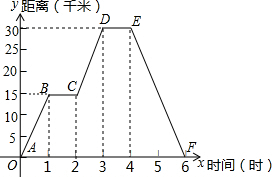 小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
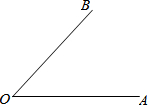 已知∠AOB(如图),求作:
已知∠AOB(如图),求作:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com