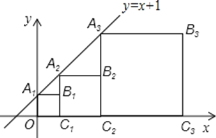
[题目]正方形...按如图的方式放置点...和点...分别在直线和x轴上.则点的坐标是．题目和参考答案——青夏教育精英家教网—

【题目】正方形，，，按如图的方式放置点，，，和点，，，分别在直线和x轴上，则点的坐标是______．

【答案】(2017,2018)

【解析】

A1的横坐标为0，把x=0代入y=x+1得：y=1，根据四边形A1B1C1O为正方形，得到A2和B1的横坐标为1，把x=1代入y=x+1得：y=2，即A3的横坐标为2，把x=2代入y=x+1得：y=3，猜想归纳出点A2018的横坐标，代入y=x+1求出纵坐标，即可得到答案．

A1的横坐标为0，把x=0代入y=x+1得：y=1．

∵四边形A1B1C1O为正方形，∴A2和B1的横坐标为1，把x=1代入y=x+1得：y=2，即A3的横坐标为2，把x=2代入y=x+1得：y=3，即A4的横坐标为3，把x=3代入y=x+1得：y=4，…

依此类推，A2018的横坐标为2017，把x=2017代入y=x+1得：y=2018，即点A2018的坐标是（2017，2018）．

故答案为：（2017，2018）．

练习册系列答案

青苹果同步评价手册系列答案

初中英语知识集锦系列答案

小学语文词语手册吉林教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】（1）解不等式：2x﹣5＜4（x+1）﹣3；

（2）解关于x的不等式：x﹣5＞a（x+4）（a≠1）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直角三角形ABC的直角边AB=6，BC=8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，DE交AC于点G，BE＝2，三角形CEG的面积为13.5，下列结论：

①三角形ABC平移的距离是4； ②EG=4.5；

③AD∥CF； ④四边形ADFC的面积为6．

其中正确的结论是（）

A. ①② B. ②③ C. ③④ D. ②④

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】认真阅读并填空：

已知：如图，∠1=∠2，∠C=∠D，试说明：∠A=∠F．

解：∵∠1=∠2（已知），∠2=∠3（）

∴∠1=∠3（等量代换）

∴BD∥EC（）

∴∠4=∠C（两直线平行，同位角相等）

又∠C=∠D（已知）

∴∠4=∠D（）

∴ ∥ （内错角相等，两直线平行）

∴∠A=∠F（）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，抛物线y＝－x 2＋bx＋c与x轴交于A、B两点，与y轴交于点C，已知经过B、C两点的直线的表达式为y＝－x＋3．

（1）求抛物线的函数表达式；
（2）点P(m，0)是线段OB上的一个动点，过点P作y轴的平行线，交直线BC于D，交抛物线于E，EF∥x轴，交直线BC于F，DG∥x轴，FG∥y轴，DG与FG交于点G．设四边形DEFG的面积为S，当m为何值时S最大，最大值是多少？
（3）在坐标平面内是否存在点Q，将△OAC绕点Q逆时针旋转90°，使得旋转后的三角形恰好有两个顶点落在抛物线上．若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．