
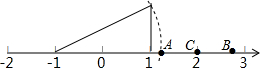
 如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$.
如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$. 科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
A. 总体 B. 个体 C. 总体的一个样本 D. 普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
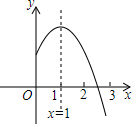 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )| A. | ①、② | B. | ①、③ | C. | ①、②、③ | D. | ①、②、④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
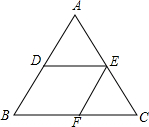 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{AD}{BD}=\frac{BF}{FC}$ | D. | $\frac{BD}{AD}=\frac{BF}{FC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com