
 ��ͼ���ڡ�ABC�У���ACB=90�㣬��ֱ�DZ�BCΪֱ���ġ�O��AB�ڵ�D������CD����CAB�Ľ�ƽ���߽�CD�ڵ�E����BC�ڵ�F������O�ڵ�P��
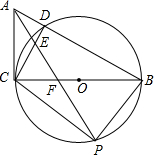
��ͼ���ڡ�ABC�У���ACB=90�㣬��ֱ�DZ�BCΪֱ���ġ�O��AB�ڵ�D������CD����CAB�Ľ�ƽ���߽�CD�ڵ�E����BC�ڵ�F������O�ڵ�P������ ��1��������ֱ�������ε����ʺ�ͬ�ǵ��������жϳ�����ACD=��ABC�������ó���ACE�ס�ABF���ɵó�$\frac{AC}{AB}$=$\frac{AE}{AF}$�����ý�ƽ���߶����ó�$\frac{AC}{AB}=\frac{CF}{BF}$�����۵�֤��
��2������������Ǻ����Ķ��壬���AC=3x���ó�BC��AC��������1���Ľ������CF���ٸ��ݹ��ɶ������AF���ɵó����ۣ�
��3������ֱ�������ε�����ǻ���ó�����BAC=60�㣬CAP=30�㣬��FCM=30�㣬��FON=30�����ú�30���ֱ�������ε����߹�ϵ���������AC=$\sqrt{3}$��CF=1��OF=$\frac{1}{2}$��ON=$\frac{\sqrt{3}}{4}$�����ù��ɶ����������PN=$\frac{\sqrt{33}}{4}$������������ε������ʽ�����ɵó����ۣ�
��� �⣺��1��֤������BC�ǡ�Oֱ����
���BDC=90�㣬
���ABC+��BCD=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCD=90�㣬
���ACD=��ABC��
�ߡ�CAB�Ľ�ƽ���߽�CD�ڵ�E����BC�ڵ�F��
���CAE=��BAF��
���ACE�ס�ABF��
��$\frac{AC}{AB}$=$\frac{AE}{AF}$��
��AF�ǡ�BAC�Ľ�ƽ���ߣ�
��$\frac{AC}{AB}=\frac{CF}{BF}$��
��$\frac{AE}{AF}$=$\frac{CF}{BF}$��
��2����Rt��ABC��tan��CAB=$\frac{BC}{AC}$=$\frac{4}{3}$��
��AC=3x����BC=4x��
���ݹ��ɶ����ã�AB=5x��
�ɣ�1��֪��$\frac{AC}{AB}=\frac{CF}{BF}$��
��$\frac{3x}{5x}=\frac{CF}{BF}$��
��$\frac{CF}{BF}=\frac{3}{5}$��
��CF+BF=BC=4x��
��CF=$\frac{3}{2}$x��BF=$\frac{5}{2}$x��
��Rt��CAF��CF=$\frac{3}{2}$x��AC=3x��
���ݹ��ɶ����ã�AF=$\sqrt{A{C}^{2}+C{F}^{2}}$=$\frac{3\sqrt{5}}{2}$x��
��sin��CAP=$\frac{CF}{AF}$=$\frac{\frac{3}{2}x}{\frac{3\sqrt{5}}{2}x}$=$\frac{\sqrt{5}}{5}$��
��3����ͼ����Rt��ABC�У���ABC=30�㣬AB=2$\sqrt{3}$��
��AC=$\frac{1}{2}$AB=$\sqrt{3}$��BC=$\sqrt{3}$AC=3����BAC=60�㣬
��OC=$\frac{1}{2}$BC=$\frac{3}{2}$��
��AF�ǡ�BAC��ƽ���ߣ�
���CAP=��BAP=$\frac{1}{2}$��BAC=30�㣬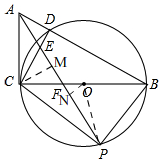 ����C��CM��AP��M����O��ON��AP��N������OP��
����C��CM��AP��M����O��ON��AP��N������OP��
��Rt��ACM�У�CM=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$����ACM=60�㣬
�ߡ�ACB=90�㣬
���FCM=��ACB-��ACM=30�㣬
��Rt��CMF�У���FCM=30�㣬CM=$\frac{\sqrt{3}}{2}$��
���CFM=90��-��FCM=60�㣬CF=1��
��OF=OC-CF=$\frac{1}{2}$��
��Rt��OFN�У���FON=90��-��OFN=30�㣬OF=$\frac{1}{2}$��
��FN=$\frac{1}{2}$OF=$\frac{1}{4}$��
��ON=$\sqrt{3}$FN=$\frac{\sqrt{3}}{4}$��
��Rt��ONP��OP=OC=$\frac{3}{2}$��ON=$\frac{\sqrt{3}}{4}$��
��PN=$\sqrt{O{P}^{2}-O{N}^{2}}$=$\frac{\sqrt{33}}{4}$��
��PF=FN+PN=$\frac{1}{4}$+$\frac{\sqrt{33}}{4}$��
��S��PCF=$\frac{1}{2}$PF•CM=$\frac{1}{2}$����$\frac{1}{4}$+$\frac{\sqrt{33}}{4}$����$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}+3\sqrt{11}}{16}$��
���PCF�������$\frac{\sqrt{3}+3\sqrt{11}}{16}$��
���� ������Բ���ۺ��⣬��Ҫ�����˽�ƽ���߶��������������ε��ж������ʣ�ֱ�������ε�����ǻ��࣬���ɶ�������30��ǵ�ֱ�������ε����ʣ�������Ǻ�����֪ʶ�㣬�Ȿ��Ĺؼ��Ǻ�30���ֱ�������ε�������ã������м�����ж��Ķ��߶γɱ������õķ�������һ���е��ѵ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15��103 | B�� | 1.5��104 | C�� | 1.5��103 | D�� | 0.15��105 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCO���Σ���BEF�ǵ���ֱ�������Σ���EBF=90�㣬��C��E��x���ϣ���A��y���ϣ���F��˫����y=$\frac{k}{x}$��k��0����һ�����ڵ�ͼ���ϣ�S��BEF=5��OC=1����k=8��
��ͼ���ı���ABCO���Σ���BEF�ǵ���ֱ�������Σ���EBF=90�㣬��C��E��x���ϣ���A��y���ϣ���F��˫����y=$\frac{k}{x}$��k��0����һ�����ڵ�ͼ���ϣ�S��BEF=5��OC=1����k=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
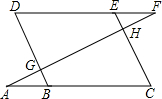 ��ͼ��ʾ����E��ֱ��DF�ϣ���B��ֱ��AC�ϣ�ֱ��AF�ֱ�BD��CE�ڵ�G��H������AGB=��EHF����C=��D���뵽�ϡ�A���F��������ϵ����˵�����ɣ�
��ͼ��ʾ����E��ֱ��DF�ϣ���B��ֱ��AC�ϣ�ֱ��AF�ֱ�BD��CE�ڵ�G��H������AGB=��EHF����C=��D���뵽�ϡ�A���F��������ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com