
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD. 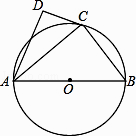
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
【答案】
(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4
(2)证明:连接OC
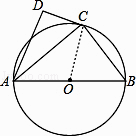
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.
【解析】(1)首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;(2)连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.


科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接![]() ,以
,以![]() 为长,
为长,![]() 为宽作矩形
为宽作矩形![]() ,且点
,且点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 也随之运动,但点
也随之运动,但点![]() 始终在反比例函数
始终在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b互为相反数,b、C互为倒数,并且m的立方等于它本身
(1)求![]() +ac值;
+ac值;
(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+![]() |,求2a-S的值.
|,求2a-S的值.
(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在,求出这个最大值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
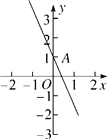
【题目】如图,在平面直角坐标系中,一次函数y=-2x+1的图象与y轴交于点A.
(1)若点A关于x轴的对称点B在一次函数y=![]() x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
(2)求这两个一次函数的图象与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
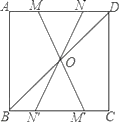
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
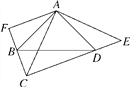
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com