
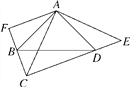
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
【答案】(1) 50;(2)证明见解析.
【解析】(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)过点A作AG⊥CD,垂足为点G,求出AF=AG,进而求出CG=AG=GE,即可得出答案.
(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAC=∠EAD.
在△ABC和△ADE中,
AB=AD,∠BAC=∠DAE,AC=AE,
∴△ABC≌△ADE(SAS).
∴S△ABC=S△ADE,∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD
=S△ACE=![]() AC·AE=
AC·AE=![]() ×102=50.
×102=50.
(2)∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°.由(1)知△ABC≌△ADE,
∴∠ACB=∠AEC=45°,∴∠ACB=∠ACE,∴CA平分∠ECF.
过点A作AG⊥CD,垂足为点G.
∵AF⊥CB,∴AF=AG.又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC,
∴CG=AG=GE,
∴CE=2AG=2AF.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,P是 ![]() 上两点,AB=13,AC=5.
上两点,AB=13,AC=5. 
(1)如图(1),若点P是 ![]() 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是 ![]() 的中点,求PA的长.
的中点,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD. 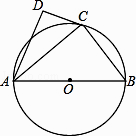
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
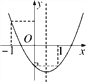
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③![]() >1;④2a+b>0.其中正确的是_______(填序号).
>1;④2a+b>0.其中正确的是_______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,但为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过400元后,超过部分按原价七折优惠;在乙超市购买商品只按原价的八折优惠;设顾客累计购物![]() 元(
元(![]() )
)
(1)用含![]() 的代数式分别表示顾客在两家超市购买所付的费用。
的代数式分别表示顾客在两家超市购买所付的费用。
(2)当![]() 时,试比较顾客到哪家超市购物更加优惠。
时,试比较顾客到哪家超市购物更加优惠。
查看答案和解析>>
科目:初中数学 来源: 题型:
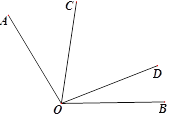
【题目】如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,下列说法:
①如果∠AOC=∠BOD,则图中有两对互补的角;
②如果作OE平分∠BOC,则∠AOC=2∠DOE;
③如果作OM平分∠AOC,且∠MON=90°,则ON平分∠BOD;
④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ,则![]() ,
,
其中正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com