
【题目】如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,下列说法:
①如果∠AOC=∠BOD,则图中有两对互补的角;
②如果作OE平分∠BOC,则∠AOC=2∠DOE;
③如果作OM平分∠AOC,且∠MON=90°,则ON平分∠BOD;
④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ,则![]() ,
,
其中正确的有( )个.
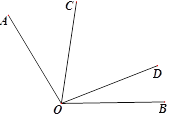
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】(1)∵∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,
∴∠AOC+∠BOD=120°-60°=60°,
又∵∠AOC=∠BOD,
∴∠AOC=∠BOD=30°,
∴∠AOD=∠BOC=30°+60°=90°,
∴∠AOD+∠BOC=180°,
又∵∠AOB+∠COD=180°,
∴图中此时有两对互补的角;故①正确;
(2)∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=
∠BOC=![]() (120°-∠AOC),
(120°-∠AOC),
∴∠DOE=![]() (120°-∠AOC)-∠BOD,
(120°-∠AOC)-∠BOD,
又∵∠BOD=120°-60°-∠AOC=60°-∠AOC,
∴∠DOE=![]() (120°-∠AOC)-∠BOD=
(120°-∠AOC)-∠BOD=![]() ∠AOC,
∠AOC,
∴∠AOC=2∠DOE;故②正确;

(3)如图,当ON在∠AOB的外部时,ON不可能平分∠BOD ,故③错误;
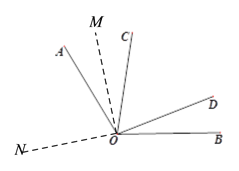
(4)∵∠AOP与∠AOC互余,∠BOQ与∠BOD互余,
∴∠AOP=90°-∠AOC,∠BOQ=90°-∠BOD,
∴∠AOP+∠BOD=180°-(∠AOC+∠BOD),
又∵∠AOC+∠BOD=120°-60°=60°,
∴∠AOP+∠BOD=180°-(∠AOC+∠BOD)=120°,
又∵∠COD=60°,
∴![]() .故④正确;
.故④正确;

综上所述,正确的说法是①②④,共3个.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
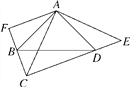
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在十月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为 4000 元/人,两家旅行社同时又对 10 人以上的团体推出了优惠举 措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位员工的费用,其余员工八 折优惠.
(1)如果设参加旅游的员工共有 n(n>10)人,则甲旅行社的费用为 元,乙旅 行社的费用为 元;(用含 n 的代数式表示)
(2)假如这个单位现组织共 30 名员工到旅游,该单位选择哪一家旅行社比较优惠?请通 过计算说明理由.
(3)如果计划在十月份外出旅游七天,这七天的日期之和(不包含月份)为 105,则他们 于十月 号出发.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O. 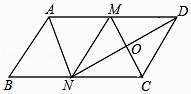
(1)求证:△ABN≌△CDM;
(2)连接MN,求证四边形MNCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l上两点A、B(点A在点B左边),且AB=10cm,在直线l上增加两点C、D(点C在点D左边),作线段AD点中点M、作线段BC点中点N;若线段MN=3 cm,则线段CD=_______cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图像大致如图2所示,则这条线段可能是图1中的( )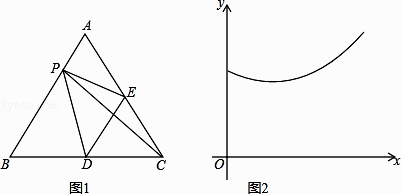
A.线段PD
B.线段PC
C.线段PE
D.线段DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com