练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1，在等边△ABC中，点E、D分别是AC，BC边的中点，点P为AB边上的一个动点，连接PE，PD，PC，DE．设AP=x，图1中某条线段的长为y，若表示y与x的函数关系的图像大致如图2所示，则这条线段可能是图1中的（ ）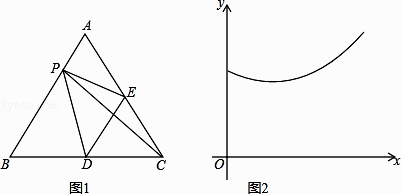

    A.线段PD
    B.线段PC
    C.线段PE
    D.线段DE

    【答案】C
    【解析】解：设边长AC=a，
    则0＜x＜a，
    根据题意和等边三角形的性质可知，
    当x= a时，线段PE有最小值；
    当x= a时，线段PC有最小值；
    当x= a时，线段PD有最小值；
    线段DE的长为定值．
    故选：C．

    【考点精析】利用函数的图象对题目进行判断即可得到答案，需要熟知函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

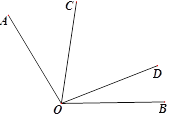
    【题目】如图，已知∠AOB=120°，∠COD在∠AOB内部且∠COD=60°，下列说法：

    ①如果∠AOC=∠BOD，则图中有两对互补的角；

    ②如果作OE平分∠BOC，则∠AOC=2∠DOE；

    ③如果作OM平分∠AOC，且∠MON=90°，则ON平分∠BOD；

    ④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ，则，

    其中正确的有（ ）个.

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了更有效地利用水资源，制定了居民用水收费标准：如果一户每月用水量不超过20立方米，每立方米按1.5元收费；如果超过20立方米，超过部分每立方米按1.8元收费，其余仍按每立方米1.5元计算，另外，超过的部分每立方米加收污水处理费1元，若某户一月份用水量（＞20）立方米，问：

    （1）该户一月份应交水费多少元？（请用含的代数式表示）

    （2）该户三月份用水量为32立方米，请问该户三月份应交水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】任何实数a，可用[a]表示不超过a的最大整数，如[4]＝4，[]＝1.现对72进行如下操作：72 []＝8 []＝2 []＝1，这样对72进行3次操作后变为1，类似地，①对81进行________次操作后变为1；②进行3次操作后变为1的所有正整数中，最大的是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：

    (1)(3a2－ab＋7)－(5ab－4a2＋7)，其中， a＝2，b＝；

    (2)3(ab－5b2＋2a2)－(7ab＋16a2－25b2)，其中|a－1|＋(b＋1)2＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热[此过程中水温y（℃）与开机时间x（分）满足一次函数关系]，当加热到100℃时自动停止加热，随后水温开始下降[此过程中水温y（℃）与开机时间x（分）成反比例关系]，当水温降至20℃时，饮水机又自动开始加热…，重复上述程序（如图所示），根据图中提供的信息，解答下列问题：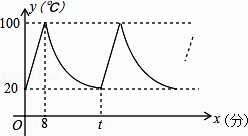
    （1）当0≤x≤8时，求水温y（℃）与开机时间x（分）的函数关系式；
    （2）求图中t的值；
    （3）若小明在通电开机后即外出散步，请你预测小明散步45分钟回到家时，饮水机内的温度约为多少℃？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．

    投资量x（万元）

    2

    种植树木利润y1（万元）

    4

    种植花卉利润y2（万元）

    2


    （1）分别求出利润y1与y2关于投资量x的函数关系式；
    （2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
    （3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

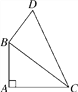
    【题目】如图所示，在四边形ABDC中，∠A＝90°，AB＝9，AC＝12，BD＝8，CD＝17.

    (1)连接BC，求BC的长；

    (2)求四边形ABDC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

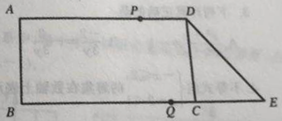
    【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

    (1)求DE的长

    (2)当t为多少时,四边形PQED成为平行四边形;

    (3)请直接写出使得△DQE是等腰三角形时t的值

    查看答案和解析>>

    同步练习册答案