
【题目】如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,求B、C两点的坐标.

【答案】点C的坐标为![]() .
.
【解析】首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.
过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
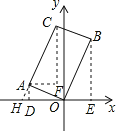
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
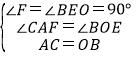 ,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4-1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴![]() ,
,
即![]() ,
,
∴OE=![]() ,
,
即点B(![]() ,3),
,3),
∴AF=OE=![]() ,
,
∴点C的横坐标为:-(2-![]() )=-
)=-![]() ,
,
∴点C(-![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=-2x+1的图象与y轴交于点A.
(1)若点A关于x轴的对称点B在一次函数y=![]() x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
(2)求这两个一次函数的图象与y轴围成的三角形的面积.
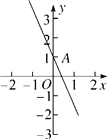
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
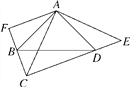
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=kx+b与反比例函数y= ![]() 的图像如图所示,则关于x的不等式kx+b﹣
的图像如图所示,则关于x的不等式kx+b﹣ ![]() ≤﹣2的解集为( )
≤﹣2的解集为( ) 
A.0<x≤2或x≤﹣4
B.﹣4≤x<0或x≥2
C.![]() ≤x<0或x
≤x<0或x ![]()
D.x ![]() 或0
或0 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
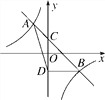
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() (k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(1)求k1、k2、m的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2、y2)是反比例函数y=![]() 图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在十月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为 4000 元/人,两家旅行社同时又对 10 人以上的团体推出了优惠举 措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位员工的费用,其余员工八 折优惠.
(1)如果设参加旅游的员工共有 n(n>10)人,则甲旅行社的费用为 元,乙旅 行社的费用为 元;(用含 n 的代数式表示)
(2)假如这个单位现组织共 30 名员工到旅游,该单位选择哪一家旅行社比较优惠?请通 过计算说明理由.
(3)如果计划在十月份外出旅游七天,这七天的日期之和(不包含月份)为 105,则他们 于十月 号出发.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com