
如图,已知抛物线![]() 与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
⑴点B的坐标为 ,点C的坐标为 (用含b的代数式表示);
⑵请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
⑶请你进一步探索在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
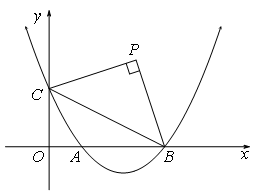
解:⑴B(b,0),C(0,![]() );
);
⑵假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.
设点P坐标(x,y),连接OP,
则![]() ,∴
,∴![]() .
.
过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,
∴∠PEO=∠EOD=∠ODP=90°. ∴四边形PEOD是矩形. ∴∠EPD=90°.
∵△PBC是等腰直角三角形,∴PC=PB,∠BPC=90°.
∴∠EPC=∠BPD.
∴△PEC≌△PDB. ∴PE=PD,即x=y.
由![]() ,解得:
,解得:![]() .
.
由△PEC≌△PDB得EC=DB,即![]() ,解得
,解得![]() 符合题意.
符合题意.
∴点P坐标为(![]() ,
,![]() ).
).
⑶假设存在这样的点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似.
∵∠QAB=∠AOQ+∠AQO,∴∠QAB>∠AOQ,∠QAB>∠AQO.
∴要使得△QOA和△QAB相似,只能∠OAQ=∠QAB=90°,即QA⊥x轴.
∵b>2,∴AB>OA. ∴∠QOA>∠QBA,∴∠QOA=∠AQB,此时∠OQB =90°.
由QA⊥x轴知QA∥y轴,∴∠COQ=∠OQA.
∴要使得△QOA和△OQC相似,只能∠OCQ=90°或∠OQC=90°.
(Ⅰ)当∠OCQ=90°时,△QOA≌△OQC. ∴AQ=CO=![]() .
.
由![]() 得:
得:![]() ,
,
解得:![]() . ∵
. ∵![]() ,∴
,∴![]() ,
,![]() .
.
∴点Q坐标为(1,![]() ).
).
(Ⅱ)当∠OQC=90°时,△QOA≌△OCQ. ∴![]() ,即
,即![]() .
.
又![]() . ∴
. ∴![]() ,即
,即![]() .
.
解得:AQ=4,此时b=17>2符合题意. ∴点Q坐标为(1,4).
∴综上可知:存在点Q(1,![]() )或(1,4),使得△QCO、△QOA和△QAB中的任意两个三角形均相似.
)或(1,4),使得△QCO、△QOA和△QAB中的任意两个三角形均相似.


科目:初中数学 来源: 题型:
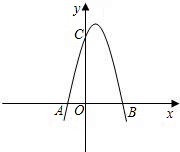 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:
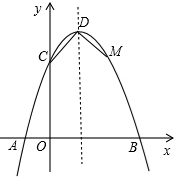 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1查看答案和解析>>
科目:初中数学 来源: 题型:
 函数的最大值是4.
函数的最大值是4.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com