
【题目】在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,垂足为点D.在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE长为( ) .
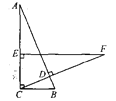
A.1cmB.2 cmC.3cmD.4cm
【答案】D
【解析】
由“∠ACB=90°,EF⊥AC”可知EF∥BC,从而可知∠BCF=∠EFC,由同角的余角相等可知∠A=∠BCF,所以∠EFC=∠A,再根据EC=BC,可知△ABC≌△FCE(AAS),从而得到对应边即可求出答案
∵∠ACB=90°,EF⊥AC,∴EF∥BC(同位角相等,两直线平行)∴∠BCF=∠EFC(两直线平行,内错角相等),∵∠B+∠A=90°,∠B+∠BCF=90°,∴∠A=∠BCF,∴∠EFC=∠A,在△ABC与△FCE中,∠EFC=∠A,∠FEC=∠ACB,EC=BC,∴△ABC≌△FCE(AAS),∴EF=AC=7,∴AE=AC-EC=7-3=4,所以选D


科目:初中数学 来源: 题型:
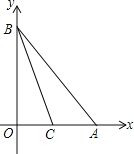
【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯市场竞争的日益激烈,为了占领市场,甲公司推出的优惠措施是:每分钟降低![]() 元后,再下调
元后,再下调![]() ;乙公司推出的优惠措施是:每分钟下调
;乙公司推出的优惠措施是:每分钟下调![]() 后,再降低
后,再降低![]() 元.已知甲、乙两公司原来每分钟收费标准相同,都是
元.已知甲、乙两公司原来每分钟收费标准相同,都是![]() 元.
元.
(1)用含![]() ,
,![]() 的式子表示甲、乙两公司推出优惠措施后每分钟的收费标准;
的式子表示甲、乙两公司推出优惠措施后每分钟的收费标准;
(2)推出优惠措施后哪家公司的收费便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 平分线,
平分线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 延长线于点
延长线于点![]() .求证:
.求证:![]() .
.
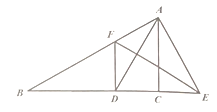
证明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分线的定义)
(角平分线的定义)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)
∴![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
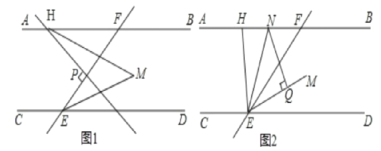
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
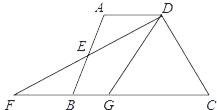
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,线段AB与A1B1的端点都在格点上.

(1)在图中建立适当的直角坐标系,使点B和B1都在x轴上,且线段AB和A1B1关于y轴成轴对称;
(2)写出点A1的坐标;
(3)若y轴上有一点P,满足PA=PB.用直尺作出点P,保留作图痕迹,并证明PA1=PB1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com