
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
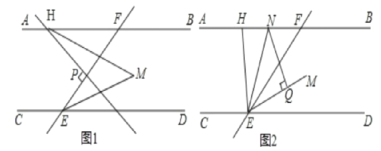
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
【答案】(1)45o (2)∠FHE=2∠ENQ或∠FHE=180°2∠ENQ,证明见解析
【解析】
(1)首先作MQ∥AB,根据平行线的性质,推得∠M=![]() (∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(2)①如图2,首先判断出∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
②如图3,首先判断出∠NEQ=∠QEF-∠NEF=![]() (∠DEF-∠HEF)=
(∠DEF-∠HEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
如图1,作MQ∥AB,
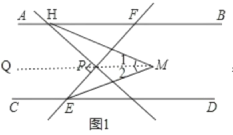
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=![]() (∠FHP+∠FED)=
(∠FHP+∠FED)= ![]() (∠FHP+∠HFP),
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°90°=90°,
∵∠1+∠2=∠M,
∴∠M=![]() ×90°=45°.
×90°=45°.
(2)①如图2,

∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,

∠FHE=180°2∠ENQ,理由如下:
∠NEQ=∠QEF∠NEF=![]() (∠DEF∠HEF)=
(∠DEF∠HEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=180°∠CEH=180°2∠ENQ.
综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.


科目:初中数学 来源: 题型:
【题目】由线段a,b,c组成的三角形不是直角三角形的是( )
A. a=15,b=8,c=17 B. a=12,b=14,c=15
C. a=![]() ,b=4,c=5 D. a=7,b=24,c=25
,b=4,c=5 D. a=7,b=24,c=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,垂足为点D.在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE长为( ) .
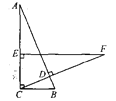
A.1cmB.2 cmC.3cmD.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,且AC在直线1上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,…,按此规律继续旋转,得到点P2018为止,则AP2018=___.
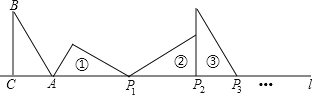
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在括号内填写理由.
已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
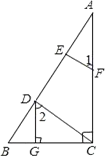
证明:∵DG⊥BC,AC⊥BC
∴∠DGB=∠ACB=90° ( )
∴DG∥AC( )
∴∠2=∠DCA ( )
∵∠1=∠2∴∠1=∠DCA
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90° 即CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= ,Sn= (用含n的式子表示).
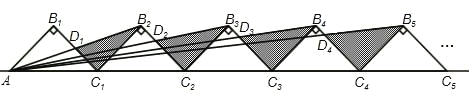
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com