
【题目】在括号内填写理由.
已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
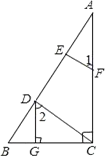
证明:∵DG⊥BC,AC⊥BC
∴∠DGB=∠ACB=90° ( )
∴DG∥AC( )
∴∠2=∠DCA ( )
∵∠1=∠2∴∠1=∠DCA
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90° 即CD⊥AB.
【答案】垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】
根据平行线的性质与判定定理即可作出解决.
证明:∵DG⊥BC,AC⊥BC
∴∠DGB=∠ACB=90° ( 垂直的定义 )
∴DG∥AC( 同位角相等,两直线平行 )
∴∠2=∠DCA ( 两直线平行,同位角相等 )
∵∠1=∠2∴∠1=∠DCA 等量代换
∴EF∥CD( 同位角相等,两直线平行 )
∴∠AEF=∠ADC( 两直线平行,同位角相等 )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90° 即CD⊥AB.

故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
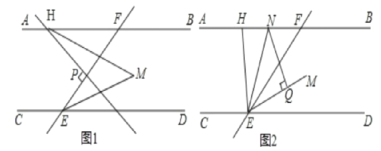
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
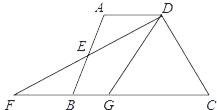
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
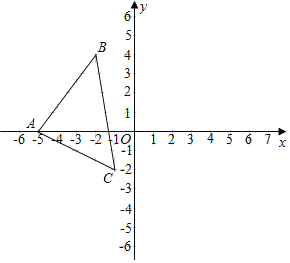
【题目】△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y轴对称.
(1)直接写出A'、B'、C'的坐标;
(2)画出△A'B'C';
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
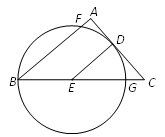
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次方程ax2+bx+c=0没有实数根,一位老师改动了方程的二次项系数后,得到的新方程有两个根为12和4;另一位老师改动原来方程的某一个系数的符号,所得到的新方程的两个根为-2和6,那么![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
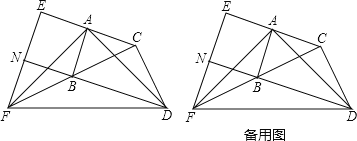
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com