
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
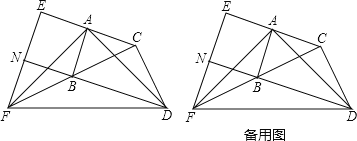
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)四边形ABNE是正方形,理由详见解析.
【解析】
试题分析:(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,求得∠ABF=135°,∠ABF=∠ACD,再证得BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
试题解析:(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
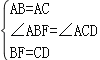 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF;
(2)证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中,
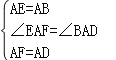 ,
,
∴△AEF≌△ABD(SAS),
∴BD=EF;
(3)解:四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
由(2)知,∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在括号内填写理由.
已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
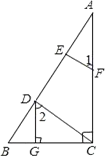
证明:∵DG⊥BC,AC⊥BC
∴∠DGB=∠ACB=90° ( )
∴DG∥AC( )
∴∠2=∠DCA ( )
∵∠1=∠2∴∠1=∠DCA
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90° 即CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= ,Sn= (用含n的式子表示).
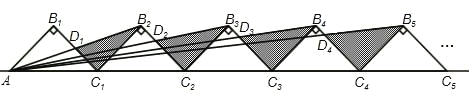
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M为双曲线y=![]() 上的一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+m于点D,C两点,若直线y=﹣x+m与y轴交于点A,与x轴相交于点B.
上的一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+m于点D,C两点,若直线y=﹣x+m与y轴交于点A,与x轴相交于点B.

(1)求ADBC的值.
(2)若直线y=﹣x+m平移后与双曲线y=![]() 交于P、Q两点,且PQ=3
交于P、Q两点,且PQ=3![]() ,求平移后m的值.
,求平移后m的值.
(3)若点M在第一象限的双曲线上运动,试说明△MPQ的面积是否存在最大值?如果存在,求出最大面积和M的坐标;如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
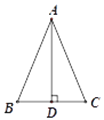
A.①②B.①②③C.①②③④D.①②③④⑤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.(能用公式计算的请用公式计算)
(1)(2)2(2018π)0+![]() ;
;
(2)(2a2)36a2a4;
(3)![]()
(4)(2a+b5) (2ab5) .
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x满足(5-x)(x-2)=2,求(x-5)2+(2-x)2的值;
解:设5-x=a,x-2=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
所以(x-5)2+(2-x)2=(5-x)2+(x-2)2=a2+b2=(a+b)2-2ab=32-2×2=5,
请仿照上面的方法求解下面的问题
(1)若x满足(9-x)(x-4)=4,求(9-x)2+(x-4)2的值;
(2)已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且AE=2,CF=4,长方形EMFD的面积是63,分别以MF、DF为边作正方形,求阴影部分的面积.
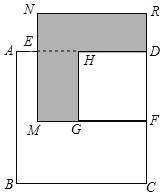
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线![]() 在
在![]() 的内部,射线
的内部,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
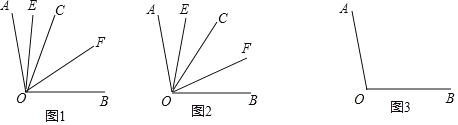
(1)如图1,若![]() ,则
,则![]() __________度;
__________度;
(2)若![]() ,
,
①如图2,若射线![]() 在
在![]() 的内部绕点
的内部绕点![]() 旋转,求
旋转,求![]() 的度数;
的度数;
②若射线![]() 在
在![]() 的外部绕点
的外部绕点![]() 旋转(旋转中
旋转(旋转中![]() 、
、![]() 均是指小于180°的角),其余条件不变,请借助图3探究
均是指小于180°的角),其余条件不变,请借助图3探究![]() 的大小,直接写出
的大小,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
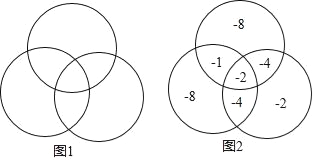
【题目】现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com