
ЁОЬтФПЁПMЮЊЫЋЧњЯпy=![]() ЩЯЕФвЛЕуЃЌЙ§ЕуMзїxжсЁЂyжсЕФДЙЯпЃЌЗжБ№НЛжБЯпy=Љx+mгкЕуDЃЌCСНЕуЃЌШєжБЯпy=Љx+mгыyжсНЛгкЕуAЃЌгыxжсЯрНЛгкЕуBЃЎ
ЩЯЕФвЛЕуЃЌЙ§ЕуMзїxжсЁЂyжсЕФДЙЯпЃЌЗжБ№НЛжБЯпy=Љx+mгкЕуDЃЌCСНЕуЃЌШєжБЯпy=Љx+mгыyжсНЛгкЕуAЃЌгыxжсЯрНЛгкЕуBЃЎ

ЃЈ1ЃЉЧѓADBCЕФжЕЃЎ
ЃЈ2ЃЉШєжБЯпy=Љx+mЦНвЦКѓгыЫЋЧњЯпy=![]() НЛгкPЁЂQСНЕуЃЌЧвPQ=3
НЛгкPЁЂQСНЕуЃЌЧвPQ=3![]() ЃЌЧѓЦНвЦКѓmЕФжЕЃЎ
ЃЌЧѓЦНвЦКѓmЕФжЕЃЎ
ЃЈ3ЃЉШєЕуMдкЕквЛЯѓЯоЕФЫЋЧњЯпЩЯдЫЖЏЃЌЪдЫЕУїЁїMPQЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШчЙћДцдкЃЌЧѓГізюДѓУцЛ§КЭMЕФзјБъЃЛШчЙћВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2![]() ЃЈ2ЃЉm=ЁР
ЃЈ2ЃЉm=ЁР![]() ЃЈ3ЃЉВЛДцдкзюДѓЕФhЃЌМДЁїMPQЕФУцЛ§ВЛДцдкзюДѓжЕ
ЃЈ3ЃЉВЛДцдкзюДѓЕФhЃЌМДЁїMPQЕФУцЛ§ВЛДцдкзюДѓжЕ
ЁОНтЮіЁП
(1) Й§CзїCEЁЭxжсгкEЃЌЙ§DзїDFЁЭyжсгкFЃЌШчЭМ1,ЧѓЕУAЃЈ0ЃЌmЃЉ; BЃЈmЃЌ0ЃЉ.ЧѓЕУЁїABOЮЊЕШбќжБНЧШ§НЧаЮЭЦГіЁїADFКЭЁїBCEвВЪЧЕШбќжБНЧШ§НЧаЮЩшM(a,b),дђab=![]() ,CE=b,DF=aНтжБНЧШ§НЧаЮМДПЩЕУЕННсТл;
,CE=b,DF=aНтжБНЧШ§НЧаЮМДПЩЕУЕННсТл;
(2) НЋy=Љx+mДњШыЫЋЧњЯпy=![]() жаЃЌећРэЕУЃКx2Љmx+
жаЃЌећРэЕУЃКx2Љmx+![]() =0ЃЌИљОнИљгыЯЕЪ§ЕФЙиЯЕЕУЕН:m=ЁР
=0ЃЌИљОнИљгыЯЕЪ§ЕФЙиЯЕЕУЕН:m=ЁР![]() ;
;
(3)гЩЩЯЪіНсТлжЊx1=y2 ЃЌ x2=y1 ЃЌЧвAO=BO=y1+y2=x1+x2=m Ђй,гЩгкx1+x2=mЃЌx1x2=![]() Ђк,ЕУЕНP,QСНЕуЕФзјБъ,ЕУЕНPQ=
Ђк,ЕУЕНP,QСНЕуЕФзјБъ,ЕУЕНPQ=![]() ,ИљОнSЁїMPQ=
,ИљОнSЁїMPQ=![]() ,ЕУЕНPQЮЊЖЈжЕ,гкЪЧЕУЕНPQБпЩЯЕФИпгазюДѓжЕЪБ,МДДцдкУцЛ§ЕФзюДѓжЕ,ЕБMЮоЯоЯђxжсгвВрдЫЖЏЪБ,(ЛђЯђyжсЕФЩЯЗНдЫЖЏЪБ)hЕФжЕЮоЯодіДѓ,гкЪЧЕУЕНВЛДцдкзюДѓЕФh,МДЁїMPQЕФУцЛ§ВЛДцдкзюДѓжЕ.
,ЕУЕНPQЮЊЖЈжЕ,гкЪЧЕУЕНPQБпЩЯЕФИпгазюДѓжЕЪБ,МДДцдкУцЛ§ЕФзюДѓжЕ,ЕБMЮоЯоЯђxжсгвВрдЫЖЏЪБ,(ЛђЯђyжсЕФЩЯЗНдЫЖЏЪБ)hЕФжЕЮоЯодіДѓ,гкЪЧЕУЕНВЛДцдкзюДѓЕФh,МДЁїMPQЕФУцЛ§ВЛДцдкзюДѓжЕ.
ЃЈ1ЃЉНтЃКЙ§CзїCEЁЭxжсгкEЃЌЙ§DзїDFЁЭyжсгкFЃЌШчЭМ1ЃЌ

ЕБx=0ЪБЃЌy=mЃЌ
ЁрAЃЈ0ЃЌmЃЉЃЛ
ЕБy=0ЪБЃЌx=mЃЌ
ЁрBЃЈmЃЌ0ЃЉЃЎ
ЁрЁїABOЮЊЕШбќжБНЧШ§НЧаЮ
ЁрЁЯOAB=ЁЯOBA=45Ёу
ЁрЁїADFКЭЁїBCEвВЪЧЕШбќжБНЧШ§НЧаЮ
ЩшMЃЈaЃЌbЃЉЃЌдђab= ![]() ЃЌCE=bЃЌDF=a
ЃЌCE=bЃЌDF=a
ЁрAD= ![]() DF=
DF= ![]() aЃЌBC=
aЃЌBC= ![]() CE=
CE= ![]() b
b
ЁрADBC= ![]() a
a ![]() b=2ab=2
b=2ab=2 ![]()
ЃЈ2ЃЉНтЃКНЋy=Љx+mДњШыЫЋЧњЯпy= ![]() жаЃЌећРэЕУЃКx2Љmx+
жаЃЌећРэЕУЃКx2Љmx+ ![]() =0ЃЌ
=0ЃЌ
Щшx1ЁЂx2ЪЧЗНГЬx2Љmx+ ![]() =0ЕФСНИіИљЃЈx1ЃМx2ЃЉЃЌ
=0ЕФСНИіИљЃЈx1ЃМx2ЃЉЃЌ
Ёрx1+x2=mЃЌx1x2= ![]() ЃЎ
ЃЎ
ЁпPQ=3 ![]() ЃЌжБЯпЕФНтЮіЪНЮЊy=Љx+mЃЌ
ЃЌжБЯпЕФНтЮіЪНЮЊy=Љx+mЃЌ
Ёрx2Љx1=3= ![]() =
= ![]() ЃЌ
ЃЌ
НтЕУЃКm=ЁР ![]()
ЃЈ3ЃЉНтЃКгЩЩЯЪіНсТлжЊx1=y2 ЃЌ x2=y1 ЃЌ ЧвAO=BO=y1+y2=x1+x2=m ЂйЃЌ
Ёпx1x2= ![]() ЂкЃЌ
ЂкЃЌ
ЁрPЃЌQСНЕуЕФзјБъПЩБэЪОЮЊPЃЈx1 ЃЌ x2ЃЉЃЌQЃЈx2 ЃЌ x1ЃЉЃЌ
ЁрPQ= ![]() ЃЈx2Љx1ЃЉЃЌ
ЃЈx2Љx1ЃЉЃЌ
ЁпЃЈx2Љx1ЃЉ2=ЃЈx1+x2ЃЉ2Љ4x1x2=m2Љ4 ![]() ЃЌ
ЃЌ
ЁрPQ= ![]()
![]() ЃЌ
ЃЌ
ЁпSЁїMPQ= ![]() PQhЃЌЁпPQЮЊЖЈжЕЃЌ
PQhЃЌЁпPQЮЊЖЈжЕЃЌ
ЁрPQБпЩЯЕФИпгазюДѓжЕЪБЃЌМДДцдкУцЛ§ЕФзюДѓжЕЃЌ
ЕБжБЯпy=Љx+mЮоЯоЯђxжсгвВрдЫЖЏЪБЃЌЃЈЛђЯђyжсЕФЩЯЗНдЫЖЏЪБЃЉhЕФжЕЮоЯодіДѓЃЌ
ЁрВЛДцдкзюДѓЕФhЃЌМДЁїMPQЕФУцЛ§ВЛДцдкзюДѓжЕЃЎ


 ЛЦИдОЕфШЄЮЖПЮЬУЯЕСаД№АИ
ЛЦИдОЕфШЄЮЖПЮЬУЯЕСаД№АИ ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
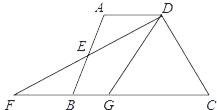
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌEЪЧABЕФжаЕуЃЌСЌНгDEВЂбгГЄНЛCBЕФбгГЄЯпгкЕуFЃЌЕуGдкБпBCЩЯЃЌЧвЁЯGDFЃНЁЯADFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїBFEЃЛ
ЃЈ2ЃЉСЌНгEGЃЌХаЖЯEGгыDFЕФЮЛжУЙиЯЕВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЖўДЮЗНГЬax2+bx+c=0УЛгаЪЕЪ§ИљЃЌвЛЮЛРЯЪІИФЖЏСЫЗНГЬЕФЖўДЮЯюЯЕЪ§КѓЃЌЕУЕНЕФаТЗНГЬгаСНИіИљЮЊ12КЭ4ЃЛСэвЛЮЛРЯЪІИФЖЏдРДЗНГЬЕФФГвЛИіЯЕЪ§ЕФЗћКХЃЌЫљЕУЕНЕФаТЗНГЬЕФСНИіИљЮЊ-2КЭ6ЃЌФЧУД![]() =________ЃЎ
=________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌЯпЖЮABгыA1B1ЕФЖЫЕуЖМдкИёЕуЩЯЃЎ

ЃЈ1ЃЉдкЭМжаНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌЪЙЕуBКЭB1ЖМдкxжсЩЯЃЌЧвЯпЖЮABКЭA1B1ЙигкyжсГЩжсЖдГЦЃЛ
ЃЈ2ЃЉаДГіЕуA1ЕФзјБъЃЛ
ЃЈ3ЃЉШєyжсЩЯгавЛЕуPЃЌТњзуPAЃНPBЃЎгУжБГпзїГіЕуPЃЌБЃСєзїЭМКлМЃЃЌВЂжЄУїPA1ЃНPB1ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
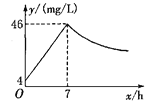
ЁОЬтФПЁПНќФъРДЃЌЮвЙњУКПѓАВШЋЪТЙЪЦЕЦЕЗЂЩњЃЌЦфжаЮЃКІзюДѓЕФЪЧЭпЫЙЃЌЦфжївЊГЩЗжЪЧCOЃЎдквЛДЮПѓФбЪТМўЕФЕїВщжаЗЂЯжЃКДгСуЪБЦ№ЃЌОЎФкПеЦјжаCOЕФХЈЖШДяЕН4 mg/LЃЌДЫКѓХЈЖШГЪжБЯпаЭдіМгЃЌдкЕк7аЁЪБДяЕНзюИпжЕ46 mg/LЃЌЗЂЩњБЌеЈЃЛБЌеЈКѓЃЌПеЦјжаЕФCOХЈЖШГЩЗДБШР§ЯТНЕЃЌШчЭМЃЌИљОнЬтжаЯрЙиаХЯЂЛиД№ЯТСаЮЪЬтЃК
(1)ЧѓБЌеЈЧАКѓПеЦјжаCOХЈЖШyгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСПШЁжЕЗЖЮЇЃЛ
(2)ЕБПеЦјжаЕФCOХЈЖШДяЕН34 mg/LЪБЃЌОЎЯТ3 kmЕФПѓЙЄНгЕНздЖЏБЈОЏаХКХЃЌетЪБЫћУЧжСЩйвЊвдЖрЩйkm/hЕФЫйЖШГЗРыВХФмдкБЌеЈЧАЬгЩњЃП
(3)ПѓЙЄжЛгадкПеЦјжаЕФCOХЈЖШНЕЕН4 mg/LМАвдЯТЪБЃЌВХФмЛиЕНПѓОЎПЊеЙЩњВњздОШЃЌЧѓПѓЙЄжСЩйдкБЌеЈКѓЖрЩйаЁЪБВХФмЯТОЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃКЂйЕШбќШ§НЧаЮЕзБпЕФжаЕуЕНСНбќЕФОрРыЯрЕШЃЛЂкЕШбќШ§НЧаЮЕФИпЁЂжаЯпЁЂНЧЦНЗжЯпЛЅЯржиКЯЃЛЂлШє![]() гы
гы![]() ГЩжсЖдГЦЃЌдђ
ГЩжсЖдГЦЃЌдђ![]() вЛЖЈгы
вЛЖЈгы![]() ШЋЕШ;ЂмгавЛИіНЧЪЧ60ЖШЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮЃЛЂнЕШбќШ§НЧаЮЕФЖдГЦжсЪЧЖЅНЧЕФЦНЗжЯпЃЎе§ШЗУќЬтЕФИіЪ§ЪЧ( )
ШЋЕШ;ЂмгавЛИіНЧЪЧ60ЖШЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮЃЛЂнЕШбќШ§НЧаЮЕФЖдГЦжсЪЧЖЅНЧЕФЦНЗжЯпЃЎе§ШЗУќЬтЕФИіЪ§ЪЧ( )
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїBCDжаЃЌЁЯBAC=ЁЯBCD=90ЁуЃЌAB=ACЃЌCB=CDЃЎбгГЄCAжСЕуEЃЌЪЙAE=ACЃЛбгГЄCBжСЕуFЃЌЪЙBF=BCЃЎСЌНгADЃЌAFЃЌDFЃЌEFЃЎбгГЄDBНЛEFгкЕуNЃЎ
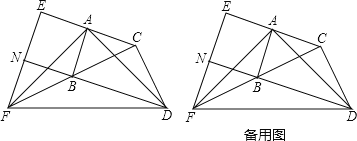
ЃЈ1ЃЉЧѓжЄЃКAD=AFЃЛ
ЃЈ2ЃЉЧѓжЄЃКBD=EFЃЛ
ЃЈ3ЃЉЪдХаЖЯЫФБпаЮABNEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЪЧЩфЯпBEЩЯвЛЕуЃЌЙ§AзїCAЁЭBEНЛЩфЯпBFгкЕуCЃЌADЁЭBFНЛЩфЯпBFгкЕуDЃЌИјГіЯТСаНсТлЃКЂйЁЯ1ЪЧЁЯBЕФгрНЧЃЛЂкЭМжаЛЅгрЕФНЧЙВга3ЖдЃЛЂлЁЯ1ЕФВЙНЧжЛгаЁЯACFЃЛЂмгыЁЯADBЛЅВЙЕФНЧЙВга3ИіЃЎдђЩЯЪіНсТле§ШЗЕФИіЪ§га( )

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABC ЮЊЕШБпШ§НЧаЮЃЌЕу DЁЂE ЗжБ№дкБп BCЁЂAC ЩЯЃЌЧв AE=CDЃЌAD гы BEЯрНЛгкЕу FЃЎдђЁЯDFE ЕФЖШЪ§ЮЊ_____ЁуЃЛ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com