
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
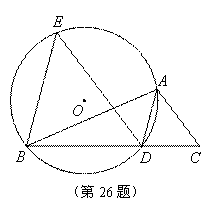 (2)若BD=2CD,设△EBD的面积为
(2)若BD=2CD,设△EBD的面积为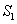 ,△ADC的面积为
,△ADC的面积为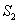 ,且
,且 ,求△ABC的面积.
,求△ABC的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在3x3的正方形网格中有四个格点A, B, C, D,,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A.A点 B. B 点 C. C点 D. D
点 C. C点 D. D 点
点

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线 与反比例函数
与反比例函数 (
( ,
,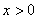 )的图象交于点A(1,
)的图象交于点A(1,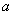 ),B是反比例函数图象上一点,直线OB与
),B是反比例函数图象上一点,直线OB与 轴的夹角为
轴的夹角为 ,
, 。21cnjy.com
。21cnjy.com
(1)求 的值;
的值;
(2)求点B的坐标;
(3)设点P( ,0),使△PAB的面积为2,求
,0),使△PAB的面积为2,求 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
将一副三角尺(在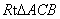 中,∠ACB=
中,∠ACB=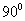 ,∠B=
,∠B=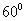 ;在
;在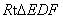 中,∠EDF=
中,∠EDF=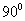 ,∠E=
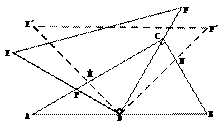
,∠E= )如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将
)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将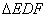 绕点D顺时针方向旋转角
绕点D顺时针方向旋转角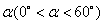 ,
, 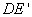 交AC于点M,
交AC于点M,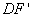 交BC于点N,则
交BC于点N,则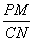 的值为
的值为
A. 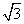 B.
B.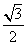 C.
C. 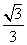 D.
D.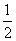
查看答案和解析>>
科目:初中数学 来源: 题型:
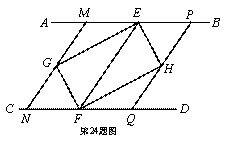
如图,AB ∥ CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1) 求证:四边形EGFH是矩形.
(2) 小明在完成(1)的证明后继续进行了探索.过G作MN ∥ EF,分别交AB、CD于点M、N,过H作PQ ∥ EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形,请在下列框图中补全他的证明思路.
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com