
【题目】如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.
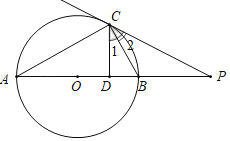
(1)求证:直线PC是⊙O的切线;
(2)若CD=4,BD=2,求线段BP的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OC,由AB是⊙O的直径证得∠ACO+∠BCO=90°,由OA=OC证得∠2=∠A=∠ACO,由此得到∠PCO=90°,即证得直线PC是⊙O的切线;
(2)利用∠1=∠A证得∠CDB=90°,得到CD2=ADBD,求出AD,由此求得AB=10,OB=5;在由∠OCP=90°推出OC2=ODOP,求出OP=![]() ,由此求得线段BP的长.
,由此求得线段BP的长.
(1)连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵OA=OC,
∴∠A=∠ACO,
∵∠A=∠1=∠2,
∴∠2=∠ACO,
∴∠2+∠BCO=90°,
∴∠PCO=90°,
∴OC⊥PC,
∴直线PC是⊙O的切线;
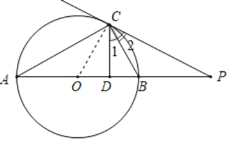
(2)∵∠ACB=90°,
∴∠A+∠ABC=90°
∴∠1=∠A,
∴∠1+∠ABC=90°,
∴∠CDB=90°,
∴CD2=ADBD,
∵CD=4,BD=2,
∴AD=8,
∴AB=10,
∴OC=OB=5,
∵∠OCP=90°,CD⊥OP,
∴OC2=ODOP,
∴52=(5﹣2)×OP,
∴OP=![]() ,
,
∴PB=OP﹣OB=![]() .
.


科目:初中数学 来源: 题型:
【题目】我校数学社团学生小明想测量学校对面斜坡![]() 上的信号树
上的信号树![]() 的高度,已知
的高度,已知![]() 的坡度为
的坡度为![]() ,且
,且![]() 的长度为65米,小明从坡底
的长度为65米,小明从坡底![]() 处沿直线走到学校大台阶底部
处沿直线走到学校大台阶底部![]() 处,
处,![]() 长为20米,他沿着与水平地面成
长为20米,他沿着与水平地面成![]() 夹角的大台阶行走20米到达平台
夹角的大台阶行走20米到达平台![]() 处,又向前走了13米到达平台上的旗杆
处,又向前走了13米到达平台上的旗杆![]() 处,此时他仰望信号树的顶部
处,此时他仰望信号树的顶部![]() ,测得仰角为
,测得仰角为![]() ,则信号树
,则信号树![]() 的高度约为( )(小明的身高忽略不计)
的高度约为( )(小明的身高忽略不计)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
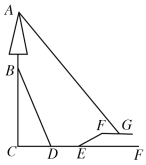
A.45米B.30米C.35米D.40米
查看答案和解析>>
科目:初中数学 来源: 题型:
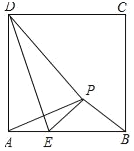
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD.
(1)作∠B的平分线交AD于E点。(用尺规作图法,保留作图痕迹,不要求写作法);
(2)若ABCD的周长为10,CD=2,求DE的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
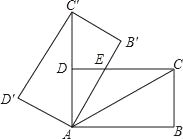
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动,与
上运动,与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若点
的左侧),若点![]() 的横坐标的最小值为0,则点
的横坐标的最小值为0,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )

A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鱼塘中养了某种鱼5000条,为了估计该鱼塘中该种鱼的总质量,从鱼塘中捕捞了3次,取得的数据如下:
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为14元,求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数关系,并估计自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com