
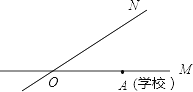
【题目】如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
【答案】18秒
【解析】
本题考查的是勾股定理的应用
点A作AC⊥ON,求出AC的长,第一台到B点时开始对学校有噪音影响,第一台到C点时,第二台到B点也开始有影响,第一台到D点,第二台到C点,直到第二台到D点噪音才消失.
如图,过点A作AC⊥ON,

∵∠MON=30°,OA=80米,
∴AC=40米,
当第一台拖拉机到B点时对学校产生噪音影响,此时AB=50,
由勾股定理得:BC=30,
第一台拖拉机到D点时噪音消失,
所以CD=30.
由于两台拖拉机相距30米,则第一台到D点时第二台在C点,还须前行30米后才对学校没有噪音影响.
所以影响时间应是:90÷5=18秒.
答:这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
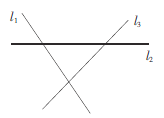
A.一处B.二处C.三处D.四处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式.
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
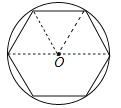
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,![]() ,那么当n=12时,π≈
,那么当n=12时,π≈![]() =______.(结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
=______.(结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
查看答案和解析>>
科目:初中数学 来源: 题型:
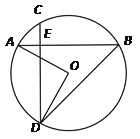
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ;(2)
;(2)![]() 的解为
的解为![]() ;
;
(3)![]() 的解为
的解为![]() ;…………
;…………
解答下列问题:
(1)请猜想:方程![]() 的解为;
的解为;
(2)请猜想:关于![]() 的方程
的方程![]() 的解为
的解为![]() (a≠0);
(a≠0);
(3)下面以解方程![]() 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.
解:原方程可化为![]() .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.

(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲品牌手机四月份售价比三月份每台降价500元.如果卖出相同数量的甲品牌手机,那么三月份销售额为9万元,四月份销售额只有8万元.
(1)四月份甲品牌手机每台售价为多少元?
(2)为了提高利润,该店计划五月份购进甲品牌及乙品牌手机销售,已知甲每台进价为3500元,乙每台进价为4000元,预算用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,问按此预算要求,可以有几种进货方案,请写出所有进货方案?
(3)该店计划五月在销售甲品牌手机时,在四月份售价基础上每售出一台甲品牌手机再返还顾客现金![]() 元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com