
【题目】科学考察队的一辆越野车需要穿越一片沙漠,但这辆车每次装满汽油最多只能行驶![]() ,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
(1)如果穿越全程大于![]() 的沙漠,在沙漠中设一个储油点
的沙漠,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点,加满油后再开往
储油点,然后返回出发点,加满油后再开往![]() ,到
,到![]() 储油点时,取出储存的所有油放在车上,再从
储油点时,取出储存的所有油放在车上,再从![]() 出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少
出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
(2)如果穿越全程大于![]() 的沙漠,在沙漠中设2个储油点
的沙漠,在沙漠中设2个储油点![]() ,
,![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到储油点
加满油,到储油点![]() 时取出储油点
时取出储油点![]() 的全部油放到车上,再到达储油点
的全部油放到车上,再到达储油点![]() ,从车中取出部分油放进
,从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到
加满油,到![]() 储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少
储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)分析越野车的行车过程,要保证车上的油最多可行驶600km,设储油点A离起点S的距离为x km,当越野车第二次回到储油点A时可以建立一个关于x的方程,解方程求出x的值,从而可求最大行程;
(2)分析越野车的行车过程,要保证车上的油最多可行驶600km,设储油点A离起点S的距离为x km,储油点B离储油点A的距离为y km,当越野车第二次回到储油点A时可以建立一个关于x的方程,当越野车第二次回到储油点B时可以建立一个关于x,y的方程,解方程组求出x,y的值,从而可求最大行程.
(1)设储油点A离起点S的距离为x km
则越野车从起点S出发到A点再回到S点,共行驶2x km,所以最多在A点放(600-2x)km路程的油,然后再一次从S点出发到点A,行驶x km,根据车上最多装行驶600km的油,则有
![]()
解得![]()
∴在A储油点放了![]() km路程的油
km路程的油
∴越野车最多行驶![]()
(2)设储油点A离起点S的距离为x km, 储油点B离储油点A的距离为y km,
当越野车第二次回到A点时有,
![]()
当越野车第二次回到B点时有,
![]()
则![]()
解得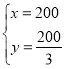
∴越野车最多行驶![]()


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数y=-x2+2x.有下列四个结论:
①它的对称轴是直线x=1;
②设y1=-x12 +2x1,y2=-x22+2x2,则当x2>x1时,有y2>y1;
③它的图象与x轴的两个交点是(0,0)和(2,0);
④当0<x<2时,y>0.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
(2)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=![]() (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)试写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入﹣购进成本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
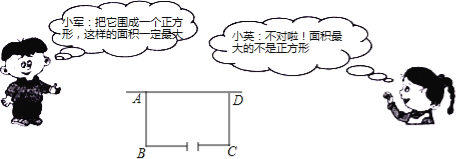
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行以“助人为乐,乐在其中”为主题的演讲比赛,比赛设一个第一名,一个第二名,两个并列第三名.前四名中七、八年级各有一名同学,九年级有两名同学,小蒙同学认为前两名是九年级同学的概率是![]() ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧.BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究:先从特殊问题开始研究:当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′,然后利用α=90°,β=30°以及等边三角形的相关知识可解决这个问题.
(1)请结合小聪研究,画出当α=90°,β=30°时相应的图形;
(2)请结合小聪研究,求出当α=90°,β=30°时∠ADB的图形;
(3)请结合小聪研究,请解决数学老师布置的这道作业题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com