Question

【题目】如图，数学老师布置了这样一道作业题：

在△ABC中，AB＝AC≠BC，点D和点A在直线BC的同侧．BD＝BC，∠BAC＝α，∠DBC＝β，α+β＝120°，连接AD，求∠ADB的度数．

小聪提供了研究：先从特殊问题开始研究：当α＝90°，β＝30°时，利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′，然后利用α＝90°，β＝30°以及等边三角形的相关知识可解决这个问题．

（1）请结合小聪研究，画出当α＝90°，β＝30°时相应的图形；

（2）请结合小聪研究，求出当α＝90°，β＝30°时∠ADB的图形；

（3）请结合小聪研究，请解决数学老师布置的这道作业题.

Answer 1

【答案】（1）见解析；（2）∠ADB＝30°；（3）∠ADB＝150°

【解析】

（1）根据题意作出图形即可；

（2）作辅助线构建全等三角形，证明△ABD≌△ABD′得△BD′C是等边三角形，再证明△AD′B≌△AD′C得∠AD′B＝∠BD′C＝30°，则∠ADB＝∠AD′B＝30°；

（3）分两种情况进行讨论：第一种情况：当60°＜α≤120°时，利用全等先求∠ABC和∠ABD的度数，从而得∠ABD′和∠D′BC的度数，得到△BD′C是等边三角形，根据（1）同理得出∠ADB＝∠AD′B＝30°；第二种情况：当0°＜α＜60°时，仍然按此过程求出∠ADB＝∠AD′B＝150°．

（1）如图1，

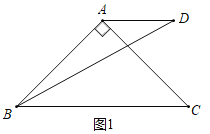
（2）如图2，作∠AB D′＝∠ABD，B D′＝BD，连接CD′，AD′，

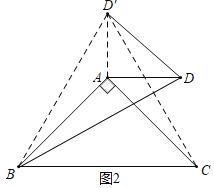
∵AB＝AC，∠BAC＝90°，

∴∠ABC＝45°，

∵∠DBC＝30°，

∴∠ABD＝∠ABC﹣∠DBC＝15°，

∵AB＝AB，∠AB D′＝∠ABD，B D′＝BD，

∴△ABD≌△ABD′（SAS），

∴∠ABD＝∠ABD′＝15°，∠ADB＝∠AD′B，

∴∠D′BC＝∠ABD′+∠ABC＝60°，

∵BD＝BD′，BD＝BC，

∴BD′＝BC，

∴△D′BC是等边三角形，

∴D′B＝D′C，∠BD′C＝60°，

∵AB＝AC，AD'＝AD'，

∴△AD′B≌△AD′C，

∴∠AD′B＝∠AD′C，

∴∠AD′B＝∠BD′C＝30°，

∴∠ADB＝30°，

（3）解：第一种情况：当60°＜α≤120°时，

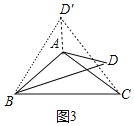
如图2，作∠AB D′＝∠ABD，B D′＝BD，连接CD′，AD′，

∵AB＝AC，

∴∠ABC＝∠ACB，

∵∠BAC＝α，

∴∠ABC＝＝90°﹣，

∴∠ABD＝∠ABC﹣∠DBC＝90°﹣﹣β，

同（1）可证△ABD≌△ABD′，

∴∠ABD＝∠ABD′＝90°﹣﹣β，BD＝BD′，∠ADB＝∠AD′B

∴∠D′BC＝∠ABD′+∠ABC＝90°﹣＝180°﹣（α+β），

∵α+β＝120°，

∴∠D′BC＝60°，

以下同（1）可求得∠ADB＝30°，

第二种情况：当0°＜α＜60°时，

如图3，

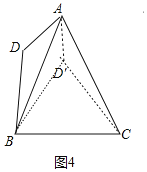
作∠AB D′＝∠ABD，B D′＝BD，连接CD′，AD′．同理可得：∠ABC＝，

∴∠ABD＝∠DBC﹣∠ABC＝，

同（1）可证△ABD≌△ABD′，

∴∠ABD＝∠ABD′═，

，BD＝BD′，∠ADB＝∠AD′B，

∴∠D′BC＝∠ABC﹣∠ABD′＝90°﹣，

∴D′B＝D′C，∠BD′C＝60°．

同（1）可证△AD′B≌△AD′C，

∴∠AD′B＝∠AD′C，

∵∠AD′B+∠AD′C+∠BD′C＝360°，

∴∠ADB＝∠AD′B＝150°．