

���� ��1��������������ٵ�PA=PBʱ���ڵ�AB=APʱ���۵�BA=BPʱ����ͼ�Ϸֱ��������������ĵ�P���ɵ��������ε����ʼ��������������¶��ǵĶ�����
��2��������������ٵ�PA=PBʱ���ɵ��������ε����ʵó���PAB=��B=45�㣬�ó���APB=90�㣬��ֱ�����������������Ǻ������PB�����ɵó������
�ڵ�AB=APʱ���ɵ��������ε����ʺ����Ǻ���������������
�۵�BP=BA=2$\sqrt{2}$ʱ�����ɵó������
��� �⣺��1������ʹ��ABP�ǵ��������ε����Σ�����ʹ��ABP�ǵ��������εĵ�P��3������ͼ��ʾ��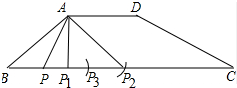
�ٵ�PA=PBʱ����PAB=��B=45�㣬
���APB=90�㣻
�ڵ�AB=APʱ����APB=��B=45�㣬
���BAP=90�㣻
�۵�BA=BPʱ������Ϊ��B=45�㣻
������������������µĶ��Ƕ���Ϊ90�㣬90�㣬45�㣻
��2�������������
�ٵ�PA=PBʱ����PAB=��B=45�㣬
���APB=90�㣬
��PA=PB=$\frac{\sqrt{2}}{2}$AB=2��
��t=2��
�ڵ�AB=APʱ����APB=��B=45�㣬
���BAP=90�㣬
��PB=$\sqrt{2}$AB=$\sqrt{2}$��$\sqrt{8}$=4��
��t=4��
�۵�BP=BA=2$\sqrt{2}$ʱ��t=2$\sqrt{2}$��
����������tΪ2��4��2$\sqrt{2}$ʱ����ABP�ǵ��������Σ�
���� �������ı����ۺ���Ŀ�����������ε����ʡ����������ε��ж������ʡ����Ǻ�����֪ʶ��������һ���Ѷȣ��ۺ���ǿ���ر�����Ҫ���з������ۣ����õ��������ε����ʺ����Ǻ������ܵó������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
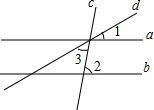 ��ͼ������ֱ��a��b��c��d������a��b����1=30�㣬��2=75�㣬���3���ڣ�������
��ͼ������ֱ��a��b��c��d������a��b����1=30�㣬��2=75�㣬���3���ڣ�������| A�� | 30�� | B�� | 40�� | C�� | 45�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | -2.5 | D�� | 2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
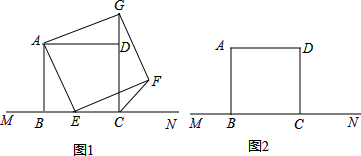
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | ������һ������ | C�� | ���Ǹ��� | D�� | ������һ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com