
【题目】“共建环保模范城,共享绿色新重庆”,市政府强力推进城市生活污水处理、生活垃圾处理设施建设改造工作.为此,某化工厂在一期工程完成后购买了4台甲型和5台乙型污水处理设备,共花费资金102万元,且每台乙型设备的价格比每台甲型设备价格少3万元.已知每台甲型设备每月能处理污水240吨,每台乙型设备每月能处理污水180吨.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共12台用于二期工程的污水处理,预算本次购买资金不超过129万元,预计二期工程完成后每月将产生不少于2220吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)请你说明在(2)的所有方案中,哪种购买方案的总花费最少?
【答案】(1)每台甲型设备是13万元,每台乙型设备的价格是10万元;(2)购买方案有:①甲型1台,乙型11台;②甲型2台,乙型10台;③甲型3台,乙型9台;(3)方案①总花费最少.
【解析】
(1)设每台甲型设备是x万元,每台乙型设备的价格是y万元,根据题意列出方程就可以求出其解.
(2)设购买甲型设备a台,乙型设备(12﹣a)台,根据题意可以建立不等式组,从而求出其解.
(3)分别计算出各种方案的费用,就可以比较出最少方案的花费.
(1)设每台甲型设备是x万元,每台乙型设备的价格是y万元,根据题意得:
![]() ,
,
解得:![]() .
.
答:每台甲型设备是13万元,每台乙型设备的价格是10万元.
(2)设购买甲型设备a(a为整数)台,乙型设备(12﹣a)台,根据题意得:
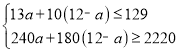 ,
,
解得:1≤a≤3,
∵a为整数,
∴a=,1,2,3.
∴购买方案有:①、甲型1台,乙型11台;
②、甲型2台,乙型10台;
③、甲型3台,乙型9台.
(3)方案①的费用为:1×13+11×10=123万元;
方案②的费用为:2×13+10×10=126万元;
方案③的费用为:3×13+9×10=129万元.
∵123<126<129,
∴方案①总花费最少.


科目:初中数学 来源: 题型:
【题目】将下列各式因式分解
(1)2a3b﹣8ab3
(2)﹣x3+x2y﹣![]() xy2
xy2
(3)(7x2+2y2)2﹣(2x2+7y2)2
(4)(x2+4x)2+(x2+4x)﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A、B 两点,交 y 轴于 C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论:①abc>0;②4a﹣2b+c>0;③5a+2c>3b;④(4a﹣b)(2a+b)<0;正确的有( )个.
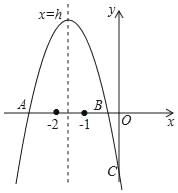
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
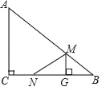
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,且MG⊥BC,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)用含t的式子表示MG;
(2)当t为何值时,四边形ACNM的面积最小?并求出最小面积;
(3)若△BMN与△ABC相似,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )
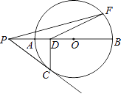
A. 2 B. ![]() C. 5:3 D. 4:3
C. 5:3 D. 4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
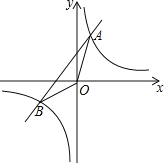
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com