
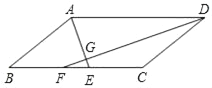
【题目】已知:如图,在ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.若AD=10,AB=6,AE=4,则DF的长为_____.
【答案】![]()
【解析】
利用相似三角形的性质求出AG,EG,再利用勾股定理求出DG,FG即可解决问题.
解:在平行四边形ABCD中,AD∥BC,BC=AD=10,
∴∠DAE=∠AEB,∠ADF=∠DFC.
∴∠BAE=∠AEB,∠CDF=∠DFC.
∵AB=DC=6,
∴BE=AB=6,FC=CD=6.
∴EC=BC﹣BE=4.
∴EF=FC﹣EC=2.
∵AD∥BC,
∴∠DAG=∠FEG,∠ADG=∠EFG.
∴△AGD∽△EGF,
∴![]() ,
,
∵AE=4,
∴AG=![]() ×4=
×4=![]() ,EG=
,EG=![]() ,
,
在平行四边形ABCD中,AB∥DC,
∴∠BAD+∠ADC=180°.
∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAE=∠BAE=![]() ∠BAD,∠ADF=∠CDF=
∠BAD,∠ADF=∠CDF=![]() ∠ADC.
∠ADC.
∴∠DAE+∠ADF=![]() ∠BAD+
∠BAD+![]() ∠ADC=90°.
∠ADC=90°.
∴∠AGD=90°.
∴DG=![]() ,FG=
,FG=![]() ,
,
∴DF=DG+FG=8![]() ,
,
故答案为8![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
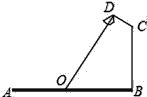
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )

A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)为弘扬 “东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
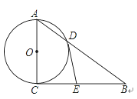
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A 市气象站测得台风中心在 A 市正东方向800 千米的B处,以50千米/时的速度向北偏西60 的 BF方向移动,距台风中心500千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
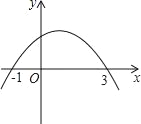
【题目】如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
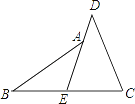
【题目】阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.
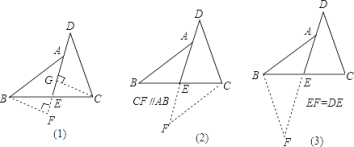
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com