
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为________.
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为________.
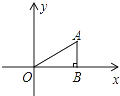
【答案】(﹣1, ![]() )或(﹣2,0)
)或(﹣2,0)
【解析】
需要分类讨论:在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标.
解:∵△ABO中,AB⊥OB,OB=![]() ,AB=1,
,AB=1,
∴tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,
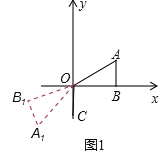
则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-1,![]() );
);
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,
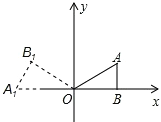
则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-2,0);
综上所述,点A1的坐标为(-1,![]() )或(-2,0);
)或(-2,0);
故答案为:(-1,![]() )或(-2,0).
)或(-2,0).


科目:初中数学 来源: 题型:
【题目】盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.
(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时,猜中的可能性大.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
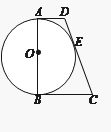
【题目】如图,AB为⊙O的直径,AD与⊙O相切于一点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
⑴求证:BC为⊙O的切线;
⑵若AB=2![]() ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省台州市)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n即为该方程的另一个实数根.
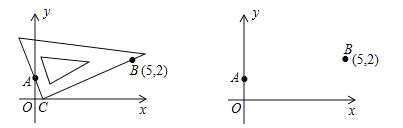
(1)在图2中,按照“第四步”的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的m就是方程![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程![]() (a≠0,
(a≠0,![]() ≥0)的实数根,请你直接写出一对固定点的坐标;
≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当m1,n1,m2,n2与a,b,c之间满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:将一把三角尺放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() .
.
探究:设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
(1)点![]() 在
在![]() 边上时,线段
边上时,线段![]() 与线段
与线段![]() 之间有怎样的大小关系?试证明你观察得到的结论(如图1);
之间有怎样的大小关系?试证明你观察得到的结论(如图1);
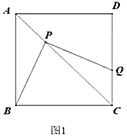
(2)点![]() 在边
在边![]() 上时设四边形
上时设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出自变量的取值范围(如图2);
之间的函数解析式,并写出自变量的取值范围(如图2);
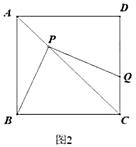
(3)点![]() 在线段
在线段![]() 上滑动时,
上滑动时,![]() 是否可能成为等腰三角形?如果可能,指出所有能使
是否可能成为等腰三角形?如果可能,指出所有能使![]() 成为等腰三角形的点
成为等腰三角形的点![]() 的位置,并直接写出相应的
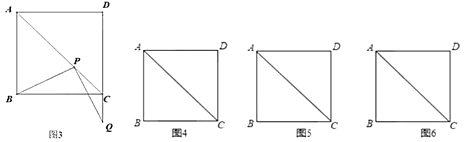
的位置,并直接写出相应的![]() 的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
查看答案和解析>>
科目:初中数学 来源: 题型:
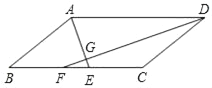
【题目】已知:如图,在ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.若AD=10,AB=6,AE=4,则DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com