
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图①,在菱形ABCD中,∠ABC=120°,点M,N分别在AD,CD上,且∠MBN=60°,试判断四边形DMBN是否为“等邻边四边形”?请说明理由.
(2)如图②,在矩形ABCD中,AB=8,BC=12.5,点E在BC上,且BE=6,在矩形ABCD内或边上,确定一点P,使四边形ABEP为最大面积的“等邻边四边形”,若能实现,请求出最大面积;若不能实现,说明理由.

【答案】(1)是,理由见解析;(2)能实现,最大面积为![]() .理由见解析.
.理由见解析.
【解析】
(1)根据题意连接BD,则有结论即四边形DMBN是“等邻边四边形”,只要证明△MBD≌△NBC即可解决问题;
(2)根据题意分以A为圆心,AB为半径画弧,当点P在![]() (不包括点I)上时和以E为圆心,EB为半径画弧,当点P在
(不包括点I)上时和以E为圆心,EB为半径画弧,当点P在![]() (不包括点H和点T)上时以及当点P在线段AE的垂直平分线上时三种情况进行讨论分析求解.
(不包括点H和点T)上时以及当点P在线段AE的垂直平分线上时三种情况进行讨论分析求解.
解:(1)结论:四边形DMBN是“等邻边四边形“.
理由:如图,连接BD,

∵四边形ABCD是菱形,∠ABC=120°,
∴∠ABD=∠CBD=60°,AB=BC=CD=AD,
∴△ABD,△BCD都是等边三角形,
∴BD=DC,∠MDB=∠C=60°,
∵∠MBN=∠DBC=60°,
∴∠MBD=∠NBC,
∴△MBD≌△NBC,
∴MB=BN,
∴四边形DMBN是“等邻边四边形“.
(2)能实现.
理由:如图,

以A为圆心,AB为半径画弧,
当点P在![]() (不包括点I)上时,四边形ABEP是“等邻边四边形“,
(不包括点I)上时,四边形ABEP是“等邻边四边形“,
点P在AD上时,当AB=AP时,四边形ABEP的面积的最大值为:![]() ;
;
以E为圆心,EB为半径画弧,
当点P在![]() (不包括点H和点T)上时,四边形ABEP是“等邻边四边形“,
(不包括点H和点T)上时,四边形ABEP是“等邻边四边形“,
有P′E⊥AE,AE=![]() ,P′E=BE=6,四边形ABEP的面积的最大值为:
,P′E=BE=6,四边形ABEP的面积的最大值为:
![]() ,
,
当点P在线段AE的垂直平分线上时,即AP=PE,易知AP=![]() ,
,
此时四边形ABEP是“等邻边四边形“,面积=![]() .
.
综上所述,等邻边四边形ABEP的面积的最大值为:![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.

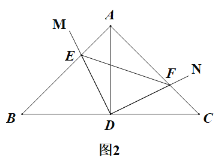
(1)求证:△ADE ≌ △CDF;
(2)求四边形AEDF的面积;
(3)如图2,连接EF,设BE=x,求△DEF的面积S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连结EF,直线EF与直线AD交于点P,设∠AEF=α°
(1)如图①,若 DE//AB,则①∠ADE的度数是_______;
②当∠DPE=∠DEP时,∠AEF= _____度:当∠PDE=∠PED,∠AEF=_______度;
(2)如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角?若存在求出α的值;若不存在,说明理由
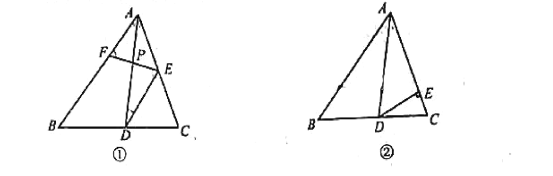
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列证明过程中的理由或步骤补充完整:
如图, EF ∥ AD , 1 2 , BAC 70 ,求 AGD 的度数.请将解题过程 填写完整.

解:∵EF∥AD(已知),
∴∠2= ______ (________________________).
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥ ______ (______________________),
∴∠BAC+ ______ =180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水蜜桃是无锡市阳山的特色水果,水蜜桃一上市,水果店的老板用2000元购进一批水密桃,很快售完;老板又用3300元购进第二批水蜜桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批水蜜桃每件进价是多少元?
(2)老板以每件65元的价格销售第二批水蜜桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批水密桃的销售利润不少于288元,剩余的仙桃每件售价最多打几折?(利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).

(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
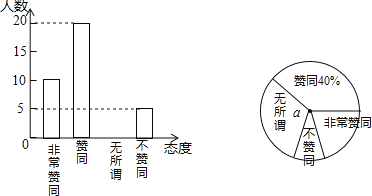
(1)在这次问卷调查中,一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 °;
(4)若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com