
【题目】已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连结EF,直线EF与直线AD交于点P,设∠AEF=α°
(1)如图①,若 DE//AB,则①∠ADE的度数是_______;
②当∠DPE=∠DEP时,∠AEF= _____度:当∠PDE=∠PED,∠AEF=_______度;
(2)如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角?若存在求出α的值;若不存在,说明理由
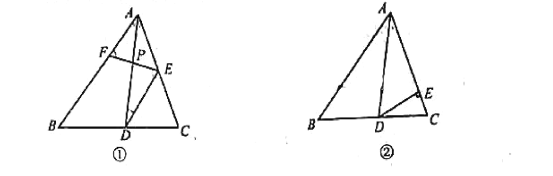
【答案】(1)①35°;②37.5,75;(2)27.5°或20°或35°.
【解析】
(1)①利用平行线的性质,可知∠ADE=∠BAD,由此即可解决问题;
②利用三角形的内角和定理以及三角形的外角的性质解决问题即可;
(2)用分类讨论的思想思考问题即可;
解:(1)①∵∠BAC=70°,AD是△ABC的角平分线,
∴∠BAD=![]() ∠BAC=35°,
∠BAC=35°,
∵DE∥AB,
∴∠ADE=∠BAD=35°,
故答案为35°.
②在△DPE中,∵∠ADE=35°,
∴∠DPE=∠PED=![]() (180°-35°)=72.5°,
(180°-35°)=72.5°,
∵∠DPE=∠AEP+∠DAE,
∴∠AEF=72.5°-35°=37.5°;
∵当∠PDE=∠PED时,∠DPE=70°,
∴∠AEF=∠DPE-∠DAE=75°.
故答案为37.5,75;
(2)在Rt△ADE中,∠ADE=90°-35°=55°.
①当DP=DE时,∠DPE=62.5°,∠AEF=∠DPE-∠DAC=62.5°-35°=27.5°.
②当EP=ED时,∠EPD=∠ADE=55°,∠AEF=∠DPE-∠DAC=55°-35°=20°.
③当DP=PE时,∠EPD=180°-2×55°=70°,∠AEF=∠DPE-∠DAC=70°-35°=35°.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
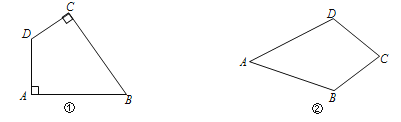
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);

(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求:
(1)CF的长;
(2)求三角形GED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人经营甲、乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品比售出的甲种商品的件数多50%时,这个商人得到的总利润率为50%;那么当售出的甲、乙两种商品的件数相等时,这个商人的总利润率是____.(利润率=利润÷成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图①,在菱形ABCD中,∠ABC=120°,点M,N分别在AD,CD上,且∠MBN=60°,试判断四边形DMBN是否为“等邻边四边形”?请说明理由.
(2)如图②,在矩形ABCD中,AB=8,BC=12.5,点E在BC上,且BE=6,在矩形ABCD内或边上,确定一点P,使四边形ABEP为最大面积的“等邻边四边形”,若能实现,请求出最大面积;若不能实现,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共调查了________名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 为正方形
为正方形![]() 的边
的边![]() 上任意一点,在正方形内部做等腰直角
上任意一点,在正方形内部做等腰直角![]() .
.


(1)如图1,若![]() ,则
,则![]() _________(请直接写出答案)
_________(请直接写出答案)
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①补全图形1;
②证明:四边形ECHF为平行四边形.
(3)在(2)的条件下,连接![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com