
【题目】某商人经营甲、乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品比售出的甲种商品的件数多50%时,这个商人得到的总利润率为50%;那么当售出的甲、乙两种商品的件数相等时,这个商人的总利润率是____.(利润率=利润÷成本)
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】(阅读材料)
南京市地铁公司规定:自2019年3月31日起,普通成人持储值卡乘坐地铁出行,每个自然月内,达到规定消费累计金额后的乘次,享受相应的折扣优惠(见图).地铁出行消费累计金额月底清零,次月重新累计.

比如:李老师二月份无储值卡消费260元,若采用新规持储值卡消费,则需付费150×0.95+50×0.9+60×0.8=235.5元.
(解决问题)
甲、乙两个成人二月份无储值卡乘坐地铁消费金额合计300元(甲消费金额超过150元,但不超过200元).若两人采用新规持储值卡消费,则共需付费283.5元.求甲、乙二月份乘坐地铁的消费金额各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C三点的坐标分别为(-2,3)(-3,1)(-5,2),将△ABC先右平移3个单位,再向下平移1个单位得到△DEF.
(1)画出△DEF,并写出点D,E,F的坐标;
(2)求△DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB=6,OC=5.点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线![]() 与y轴平行,直线
与y轴平行,直线![]() 交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线
交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线![]() 恰好过点C.
恰好过点C.
(1)求点A和点B的坐标;
(2)当0<t<3时,求m关于t的函数关系式;
(3)当m=3.5时,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连结EF,直线EF与直线AD交于点P,设∠AEF=α°
(1)如图①,若 DE//AB,则①∠ADE的度数是_______;
②当∠DPE=∠DEP时,∠AEF= _____度:当∠PDE=∠PED,∠AEF=_______度;
(2)如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角?若存在求出α的值;若不存在,说明理由
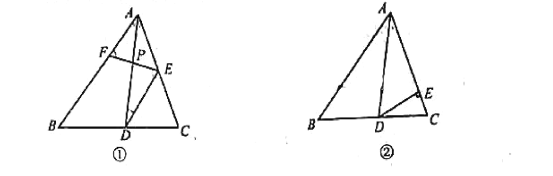
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com